9  主成分分析

在医学研究中，为了客观、全面地分析问题，常要记录多个观察指标并考虑众多的影响因素，这样的数据虽然可以提供丰富的信息，但同时也使得数据的分析工作更趋复杂化。

例如，在儿童生长发育的评价中，收集到的数据包括每一儿童的身高、体重、胸围、头围、坐高、肺活量等十多个指标。怎样利用这类多指标的数据对每一儿童的生长发育水平作出正确的评价？如果仅用其中任一指标来作评价，其结论显然是片面的，而且不能充分利用已有的数据信息。如果分别利用每一指标进行评价，然后再综合各指标评价的结论，这样做一是可能会出现各指标评价的结论不一致，甚至相互冲突，从而给最后的综合评价带来困难；二是工作量明显增大，不利于进一步的统计分析。

事实上，在实际工作中，所涉及的众多指标之间经常是有相互联系和影响的，从这一点出发，希望通过对原始指标相互关系的研究，找出少数几个综合指标，这些综合指标是原始指标的线性组合，它既保留了原始指标的主要信息，且又互不相关。这样一种从众多原始指标之间相互关系入手，寻找少数综合指标以概括原始指标信息的多元统计方法称为主成分分析。

关于特征值、特征向量、方差贡献率、累积方差贡献率等概念，大家可以阅读网络教程或者课本等。

9.1 加载数据

使用R语言自带的iris鸢尾花数据进行演示。

str(iris)
## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
psych::headTail(iris)
##     Sepal.Length Sepal.Width Petal.Length Petal.Width   Species
## 1            5.1         3.5          1.4         0.2    setosa
## 2            4.9           3          1.4         0.2    setosa
## 3            4.7         3.2          1.3         0.2    setosa
## 4            4.6         3.1          1.5         0.2    setosa
## ...          ...         ...          ...         ...      <NA>
## 147          6.3         2.5            5         1.9 virginica
## 148          6.5           3          5.2           2 virginica
## 149          6.2         3.4          5.4         2.3 virginica
## 150          5.9           3          5.1         1.8 virginica

首先给大家介绍下R自带的主成分分析函数。

9.2 相关性检验

在进行PCA之前可以先进行相关性分析，看看相关系数：

cor(iris[,-5])
##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length    1.0000000  -0.1175698    0.8717538   0.8179411
## Sepal.Width    -0.1175698   1.0000000   -0.4284401  -0.3661259
## Petal.Length    0.8717538  -0.4284401    1.0000000   0.9628654
## Petal.Width     0.8179411  -0.3661259    0.9628654   1.0000000

9.3 KMO和Bartlett球形检验

使用psych实现，关于这两个检验的解读大家自行学习~

psych::KMO(iris[,-5])
## Kaiser-Meyer-Olkin factor adequacy
## Call: psych::KMO(r = iris[, -5])
## Overall MSA =  0.54
## MSA for each item = 
## Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
##         0.58         0.27         0.53         0.63

这个检验主要反应样本量够不够，Overall MSA是总体的检验统计量，然后是每个变量的检验统计量。 MSA越大越好。一般要求大于0.5才可以（没有绝对标准，根据实际情况来）。

psych::cortest.bartlett(iris[,-5])
## R was not square, finding R from data
## $chisq
## [1] 706.9592
## 
## $p.value
## [1] 1.92268e-149
## 
## $df
## [1] 6

p.value小于0.05，表明数据可以进行主成分分析。

9.4 R自带的PCA

主成分的实现可以通过分步计算，主要就是标准化-求相关矩阵-计算特征值和特征向量。

R中自带了prcomp()进行主成分分析，这就是工具的魅力，一次完成多步需求。

使用prcomp()进行主成分分析：

# R自带函数
pca.res <- prcomp(iris[,-5], scale. = T, # 标准化
                  center = T # 中心化
                  )

# 查看标准差、特征向量（回归系数）
pca.res
## Standard deviations (1, .., p=4):
## [1] 1.7083611 0.9560494 0.3830886 0.1439265
## 
## Rotation (n x k) = (4 x 4):
##                     PC1         PC2        PC3        PC4
## Sepal.Length  0.5210659 -0.37741762  0.7195664  0.2612863
## Sepal.Width  -0.2693474 -0.92329566 -0.2443818 -0.1235096
## Petal.Length  0.5804131 -0.02449161 -0.1421264 -0.8014492
## Petal.Width   0.5648565 -0.06694199 -0.6342727  0.5235971

主成分就是根据这几个系数(这几个系数也叫主成分载荷)算出来的：(这两个并不是一个概念，只是因为数据计算导致此时恰好相等而已，这里的Rotation就是载荷矩阵)

PC1 = 0.5210659Sepal.Length - 0.2693474Sepal.Width + 0.5804131Petal.Length + 0.5648565Petal.Width

后面的主成分计算方法以此类推。

# 样本得分score（这个应该是PCA之后每个点的坐标）
head(pca.res$x)
##            PC1        PC2         PC3          PC4
## [1,] -2.257141 -0.4784238  0.12727962  0.024087508
## [2,] -2.074013  0.6718827  0.23382552  0.102662845
## [3,] -2.356335  0.3407664 -0.04405390  0.028282305
## [4,] -2.291707  0.5953999 -0.09098530 -0.065735340
## [5,] -2.381863 -0.6446757 -0.01568565 -0.035802870
## [6,] -2.068701 -1.4842053 -0.02687825  0.006586116
pca.res$center
## Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
##     5.843333     3.057333     3.758000     1.199333
# 查看标准差、方差贡献率、累积方差贡献率
summary(pca.res)
## Importance of components:
##                           PC1    PC2     PC3     PC4
## Standard deviation     1.7084 0.9560 0.38309 0.14393
## Proportion of Variance 0.7296 0.2285 0.03669 0.00518
## Cumulative Proportion  0.7296 0.9581 0.99482 1.00000
  • Standard deviation:标准差
  • Proportion of Variance:方差贡献率
  • Cumulative Proportion:累积方差贡献率

关于主成分分析中的各种术语解读，我推荐知乎上的一篇文章：主成分分析各类术语的白话解读

9.5 结果可视化

默认的主成分分析结果可视化：

biplot(pca.res)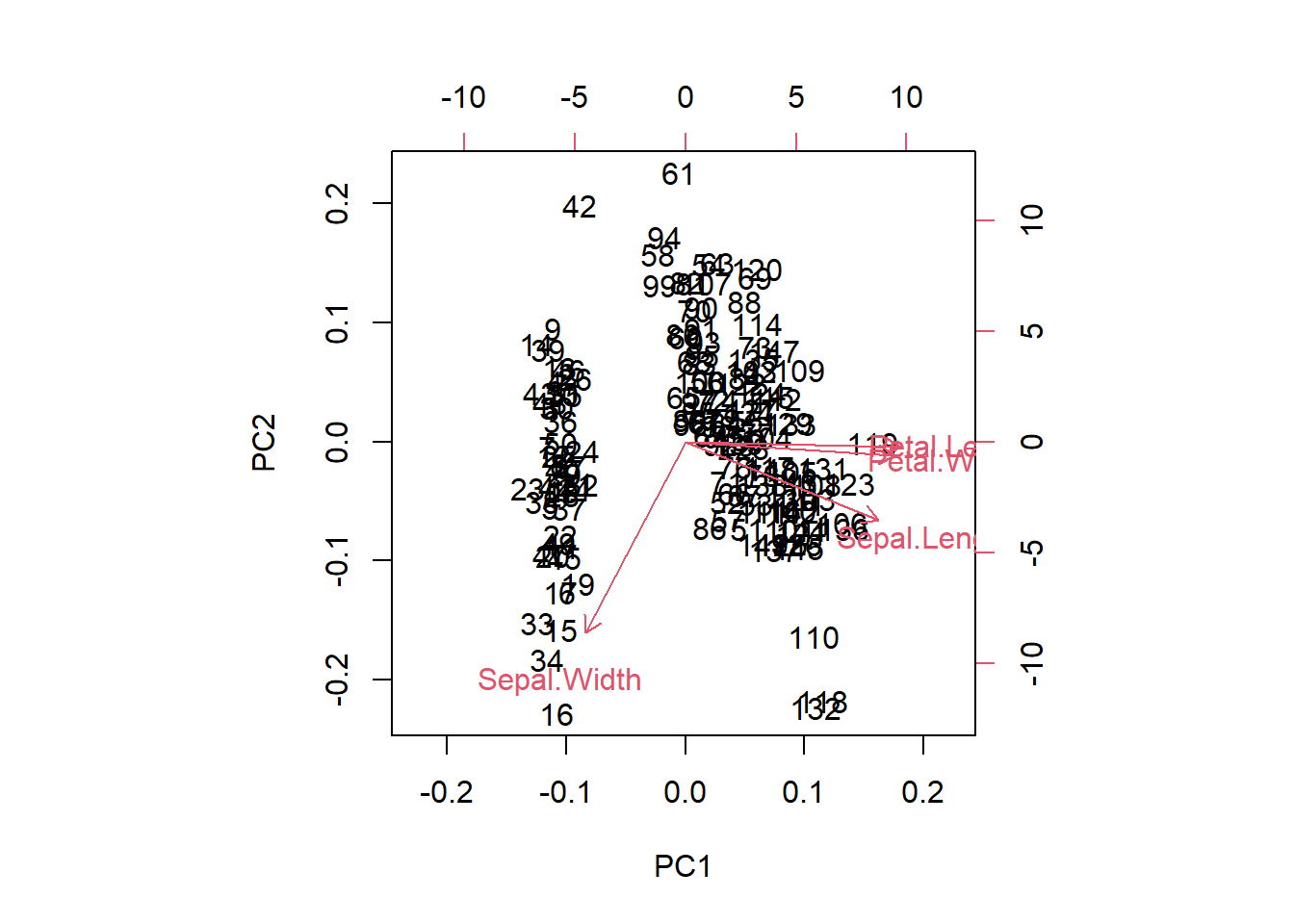

碎石图可以帮助确认最佳的主成分个数，可以使用默认的screeplot()实现：

# 默认是条形图，我们改为折线图，其实就是方差贡献度的可视化
screeplot(pca.res, type = "lines")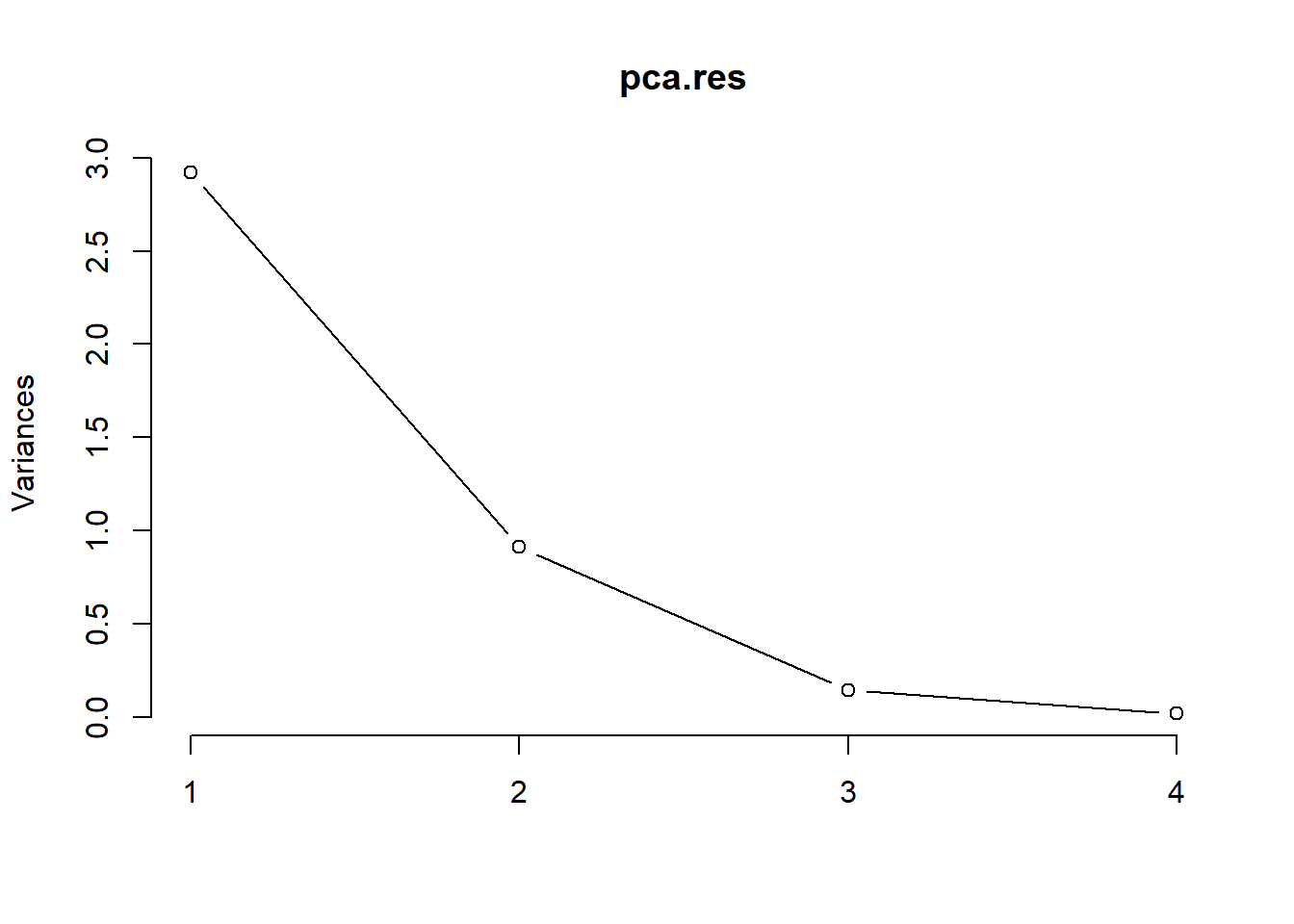

可以看到用2-3个主成分就挺好了。

一般来说，主成分的保留个数可以按照以下原则确定： 1. 以累积贡献率确定，当前K个主成分的累积贡献率达到某一特定值（一般选70%或者80%都行）时，则保留前K个主成分； 2. 以特征值大小来确定：如果主成分的特征值大于1，就保留这个主成分。

但是保留几个主成分并没有绝对的标准，大家根据自己的实际情况来！