11 多元线性回归

医学研究中许多疾病都有多种原因，而且预后也是由多种因素决定的。如糖尿病患者的血糖变化可能受胰岛素、糖化血红蛋白、血清总胆固醇、甘油三酯等多种生化指标的影响。即使对那些已知是由单一病原体导致的感染性疾病，也有许多因素影响是否发病，如遗传特征、感染途径及程度、自身免疫能力等。由于各因素间往往相互联系，多变量回归分析可以帮助我们分析变量间的数量依存关系，以及它们对结果变量的相对作用大小。多元线性回归(multiple linear regression），用于分析一个因变量与多个自变量之间的线性关系。

11.1 建立模型

使用一个医学中常见的数据进行演示：探索不同因素对空腹血糖的影响，数据录入如下：

df15_1 <- data.frame(
  cho = c(5.68,3.79,6.02,4.85,4.60,6.05,4.90,7.08,3.85,4.65,4.59,4.29,7.97,
      6.19,6.13,5.71,6.40,6.06,5.09,6.13,5.78,5.43,6.50,7.98,11.54,5.84,
      3.84),
  tg = c(1.90,1.64,3.56,1.07,2.32,0.64,8.50,3.00,2.11,0.63,1.97,1.97,1.93,
      1.18,2.06,1.78,2.40,3.67,1.03,1.71,3.36,1.13,6.21,7.92,10.89,0.92,
      1.20),
  ri = c(4.53, 7.32,6.95,5.88,4.05,1.42,12.60,6.75,16.28,6.59,3.61,6.61,7.57,
      1.42,10.35,8.53,4.53,12.79,2.53,5.28,2.96,4.31,3.47,3.37,1.20,8.61,
      6.45),
  hba = c(8.2,6.9,10.8,8.3,7.5,13.6,8.5,11.5,7.9,7.1,8.7,7.8,9.9,6.9,10.5,8.0,
      10.3,7.1,8.9,9.9,8.0,11.3,12.3,9.8,10.5,6.4,9.6),
  fpg = c(11.2,8.8,12.3,11.6,13.4,18.3,11.1,12.1,9.6,8.4,9.3,10.6,8.4,9.6,10.9,
     10.1,14.8,9.1,10.8,10.2,13.6,14.9,16.0,13.2,20.0,13.3,10.4)
  )

str(df15_1)
## 'data.frame':    27 obs. of  5 variables:
##  $ cho: num  5.68 3.79 6.02 4.85 4.6 6.05 4.9 7.08 3.85 4.65 ...
##  $ tg : num  1.9 1.64 3.56 1.07 2.32 0.64 8.5 3 2.11 0.63 ...
##  $ ri : num  4.53 7.32 6.95 5.88 4.05 ...
##  $ hba: num  8.2 6.9 10.8 8.3 7.5 13.6 8.5 11.5 7.9 7.1 ...
##  $ fpg: num  11.2 8.8 12.3 11.6 13.4 18.3 11.1 12.1 9.6 8.4 ...
head(df15_1)
##    cho   tg   ri  hba  fpg
## 1 5.68 1.90 4.53  8.2 11.2
## 2 3.79 1.64 7.32  6.9  8.8
## 3 6.02 3.56 6.95 10.8 12.3
## 4 4.85 1.07 5.88  8.3 11.6
## 5 4.60 2.32 4.05  7.5 13.4
## 6 6.05 0.64 1.42 13.6 18.3

数据一共5列，第1列是总胆固醇，第2列是甘油三酯，第3列是胰岛素，第4列是糖化血红蛋白，第5列是空腹血糖（因变量）。

在建立回归方程前，先简单探索下数据：

library(GGally)
## Warning: package 'GGally' was built under R version 4.3.3

ggpairs(df15_1) + theme_bw()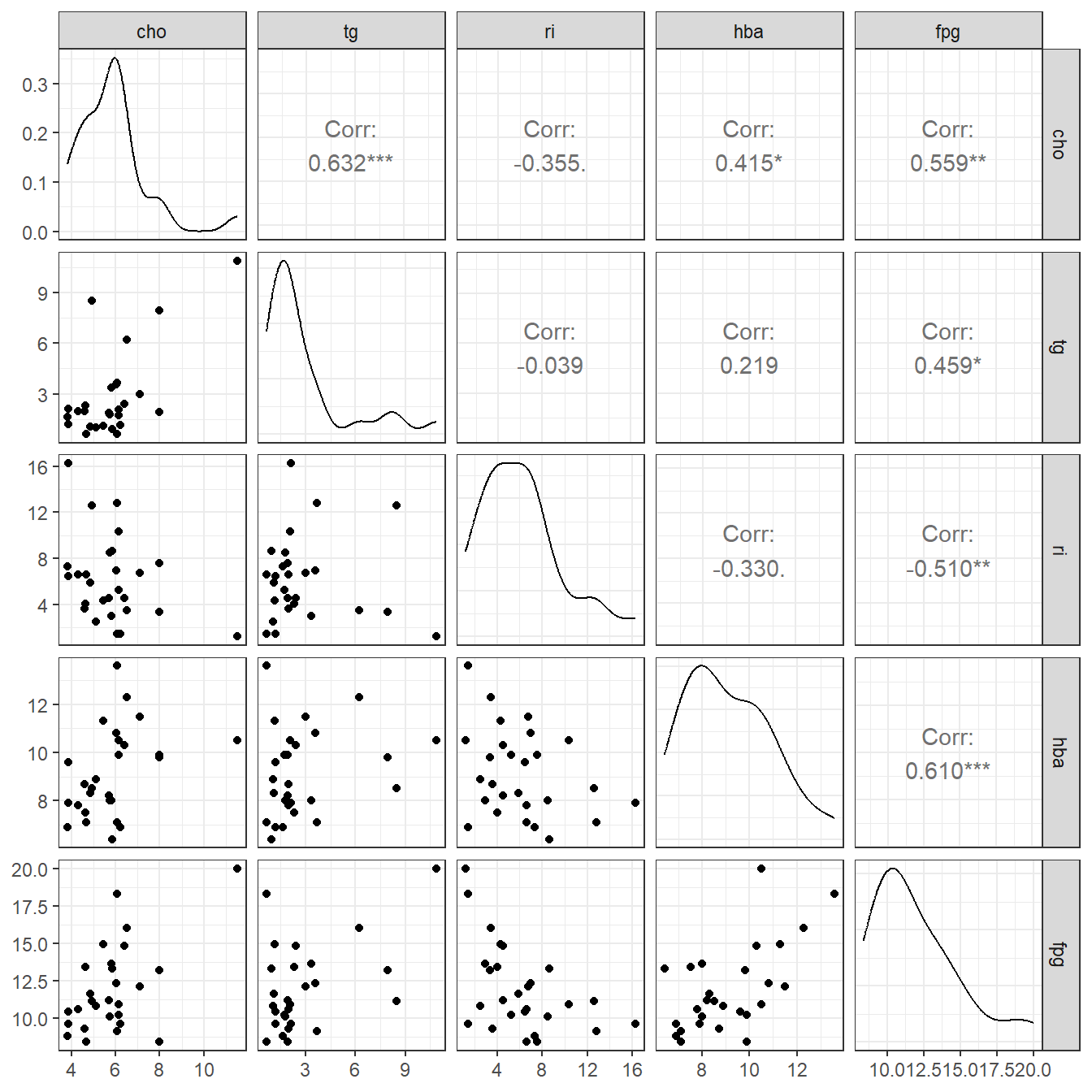

从这幅图来看，血糖和糖化血红蛋白相关性最大，和甘油三酯关系最小。

接下来建立回归方程：

f <- lm(fpg ~ cho + tg + ri + hba, data = df15_1)

summary(f)
## 
## Call:
## lm(formula = fpg ~ cho + tg + ri + hba, data = df15_1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.6268 -1.2004 -0.2276  1.5389  4.4467 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)   5.9433     2.8286   2.101   0.0473 *
## cho           0.1424     0.3657   0.390   0.7006  
## tg            0.3515     0.2042   1.721   0.0993 .
## ri           -0.2706     0.1214  -2.229   0.0363 *
## hba           0.6382     0.2433   2.623   0.0155 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.01 on 22 degrees of freedom
## Multiple R-squared:  0.6008, Adjusted R-squared:  0.5282 
## F-statistic: 8.278 on 4 and 22 DF,  p-value: 0.0003121

这个结果信息很丰富，给出了截距，各自变量的系数以及标准误、t值、P值，最下方给出了决定系数 R²，调整后的 R²，F值，总体方程的P值等。

11.2 模型评价

回归模型可以通过 R²、AIC、BIC、RMSE等评价，R²范围在0~1之间，越接近1说明结果越好。AIC、BIC、RMSE是越小越好。

library(performance)
r2(f)
## # R2 for Linear Regression
##        R2: 0.601
##   adj. R2: 0.528
AIC(f)
## [1] 120.78
BIC(f)
## [1] 128.5551
rmse(f)
## [1] 1.81395

或者直接输出所有结果：

model_performance(f)
## # Indices of model performance
## 
## AIC     |    AICc |     BIC |    R2 | R2 (adj.) |  RMSE | Sigma
## ---------------------------------------------------------------
## 120.780 | 124.980 | 128.555 | 0.601 |     0.528 | 1.814 | 2.010

11.3 回归诊断

判断数据是否满足多元线性回归的条件，也就是4个条件：

正态性
独立性
等方差性
线性

可以通过回归诊断图判断。

opar <- par(mfrow = c(2,2))

plot(f)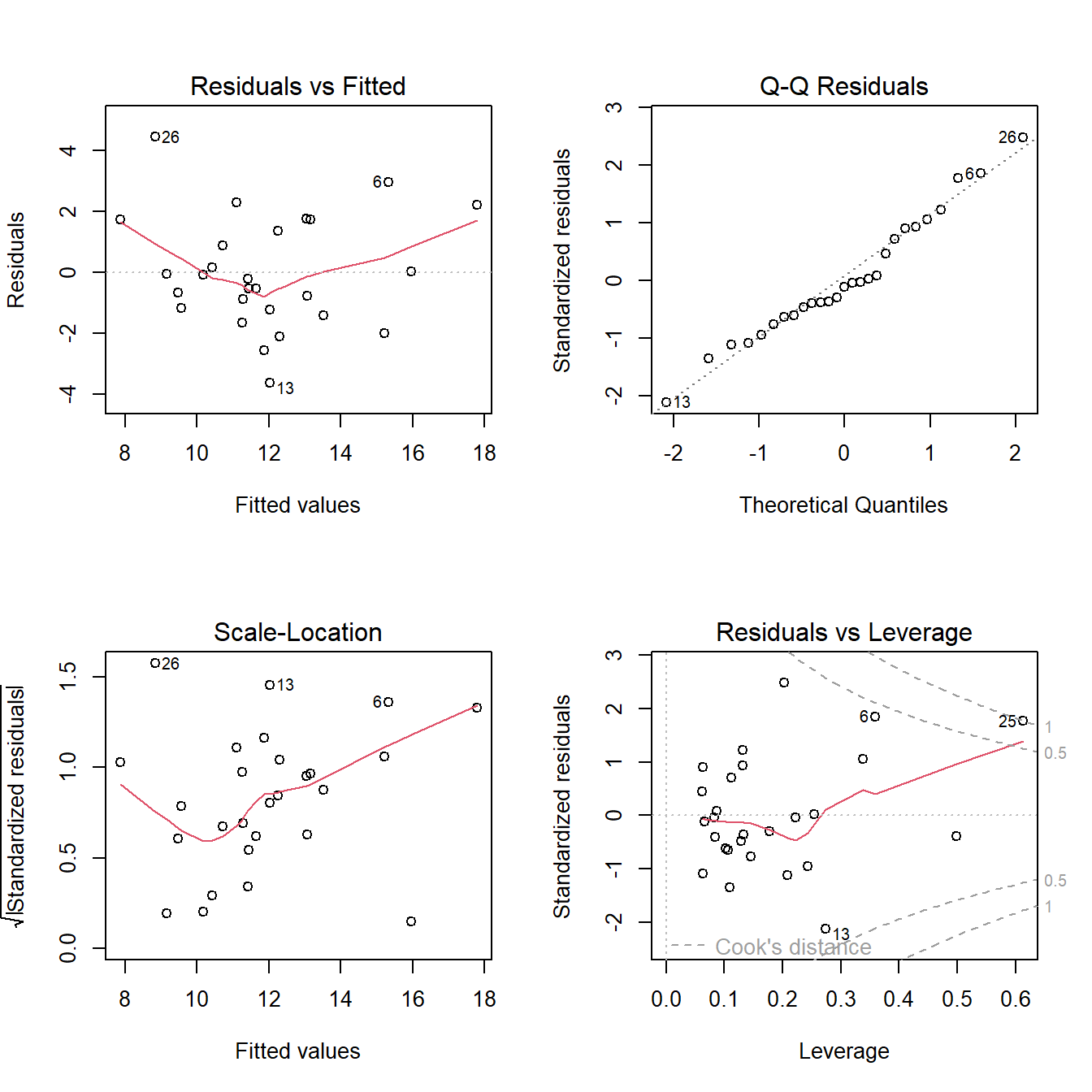


par(opar)

第1幅图（左上）是残差拟合图，展示真实残差和拟合残差的关系，判读是否满足线性这个条件，如果满足，则应该为一条直线，但是本图明显是一条曲线，说明不是很满足线性这个条件，可能需要加二次项。
第2幅图（右上）是正态Q-Q图，判断是否满足正态性这个条件，通过这个图来看，基本满足。
第3幅图（左下）是位置尺度图，判读是否满足同方差性，如果满足，水平线两侧的点应该随机分布，从此图来看基本满足。
第4幅图（右下）是残差杠杆图，用于识别离群点等。

上面是比较原始的方法，下面介绍一个非常现代化的R包，用于实现以上图形：

library(performance)
check_model(f)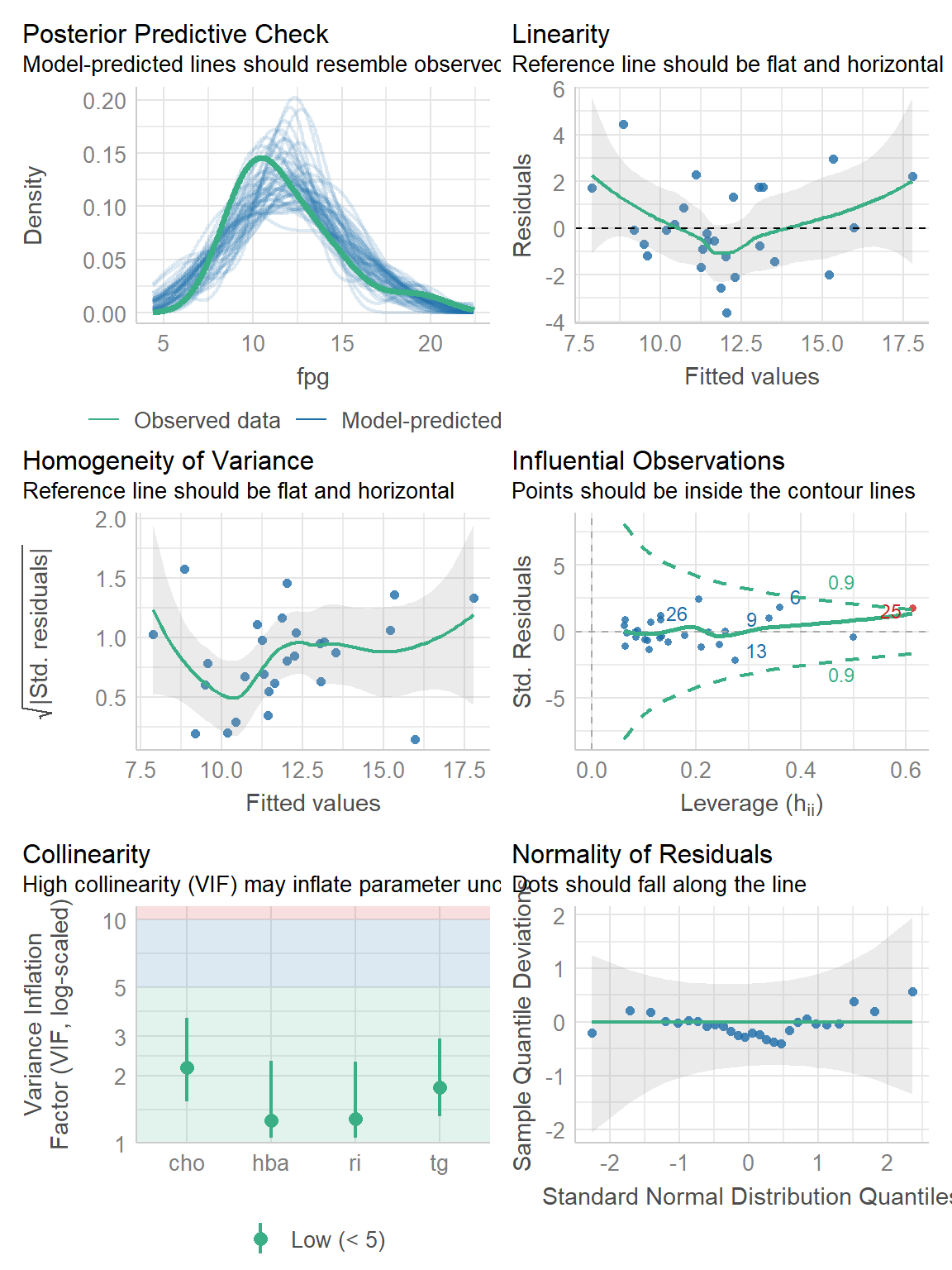

是不是更加好看了呢？

这几个图也可以单独画出来，使用以下代码即可：

diagnostic_plots <- plot(check_model(f, panel = FALSE))

首先看第一个图。这个图是基于check_predictions()函数的，属于事后检验，是检查真实数据和模型数据的拟合情况的。下图中绿色粗线是真实的预测变量的分布情况，蓝色线条表示模拟的分布，理想的情况应该是完全重合的。从下图来看，其实是有些问题的，这说明我们用的模型可能不太合适。

diagnostic_plots[[1]]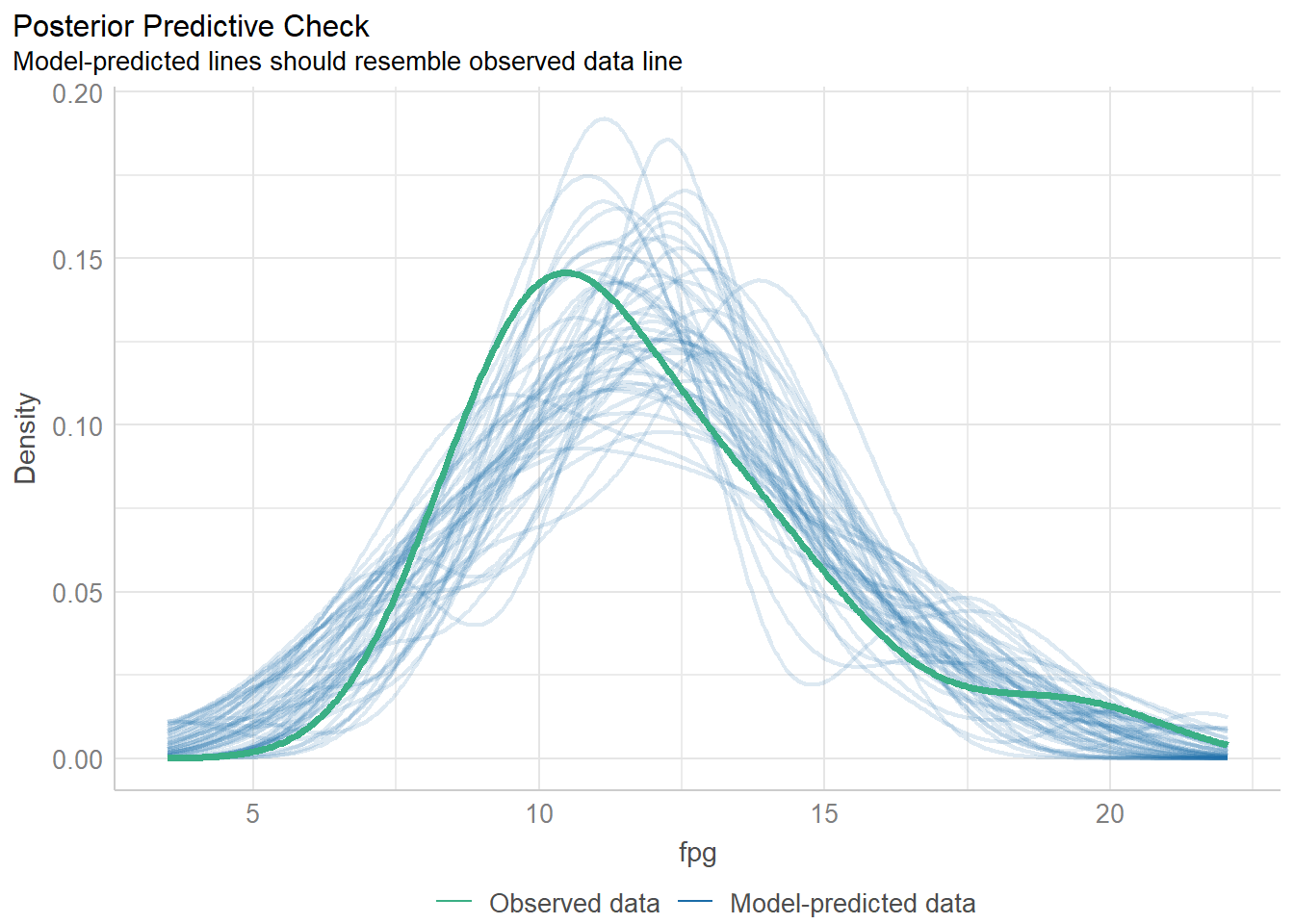

下面看第2张图。这张图是检查预测变量和结果变量是否符合线性关系的。合理的情况是残差完全随机地分布在参考线两侧。从这张图来看我们的数据其实不太完美。

diagnostic_plots[[2]]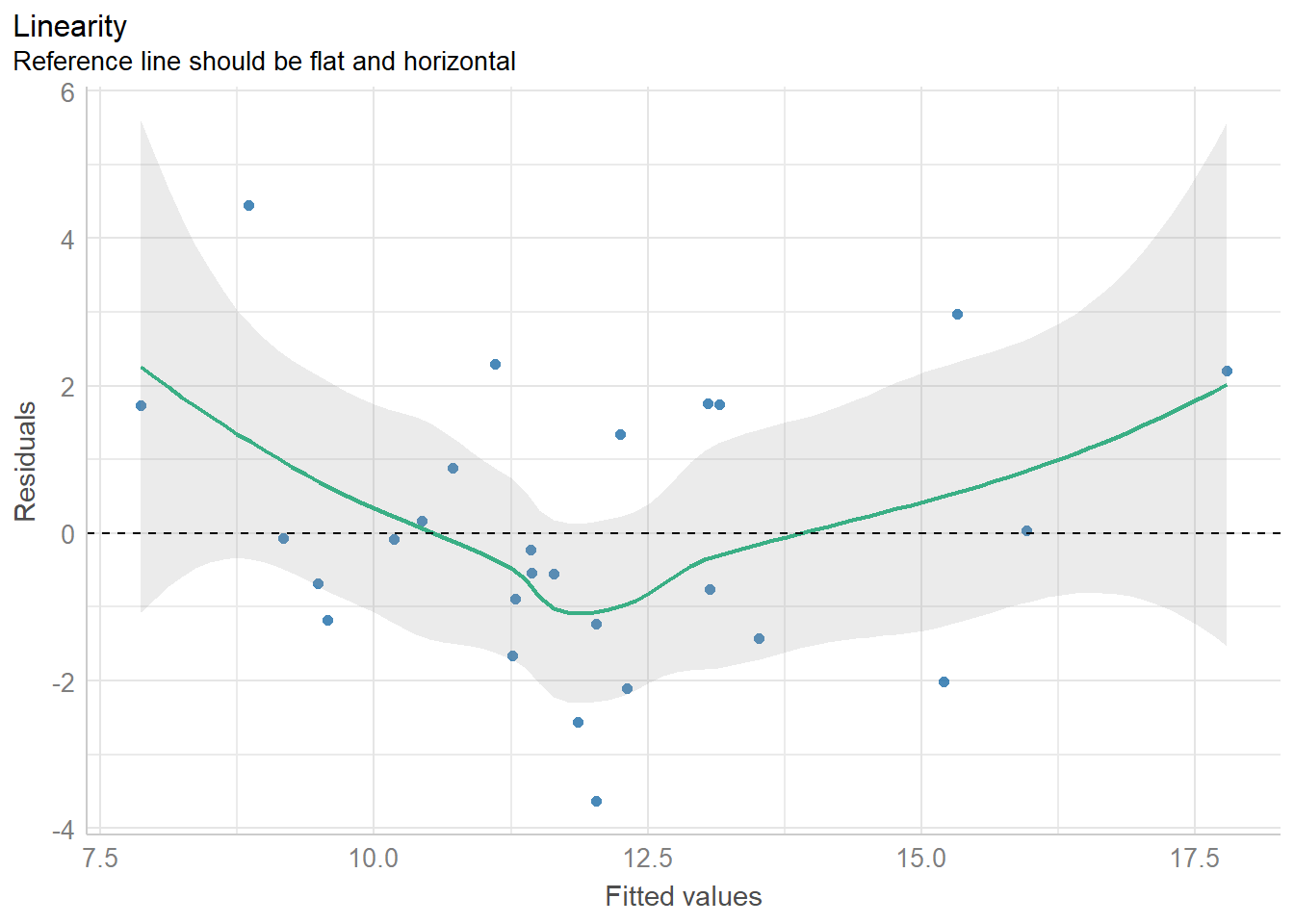

下面是第3幅图，是用来检查方差齐性的，同上面介绍过的位置尺度图。

diagnostic_plots[[3]]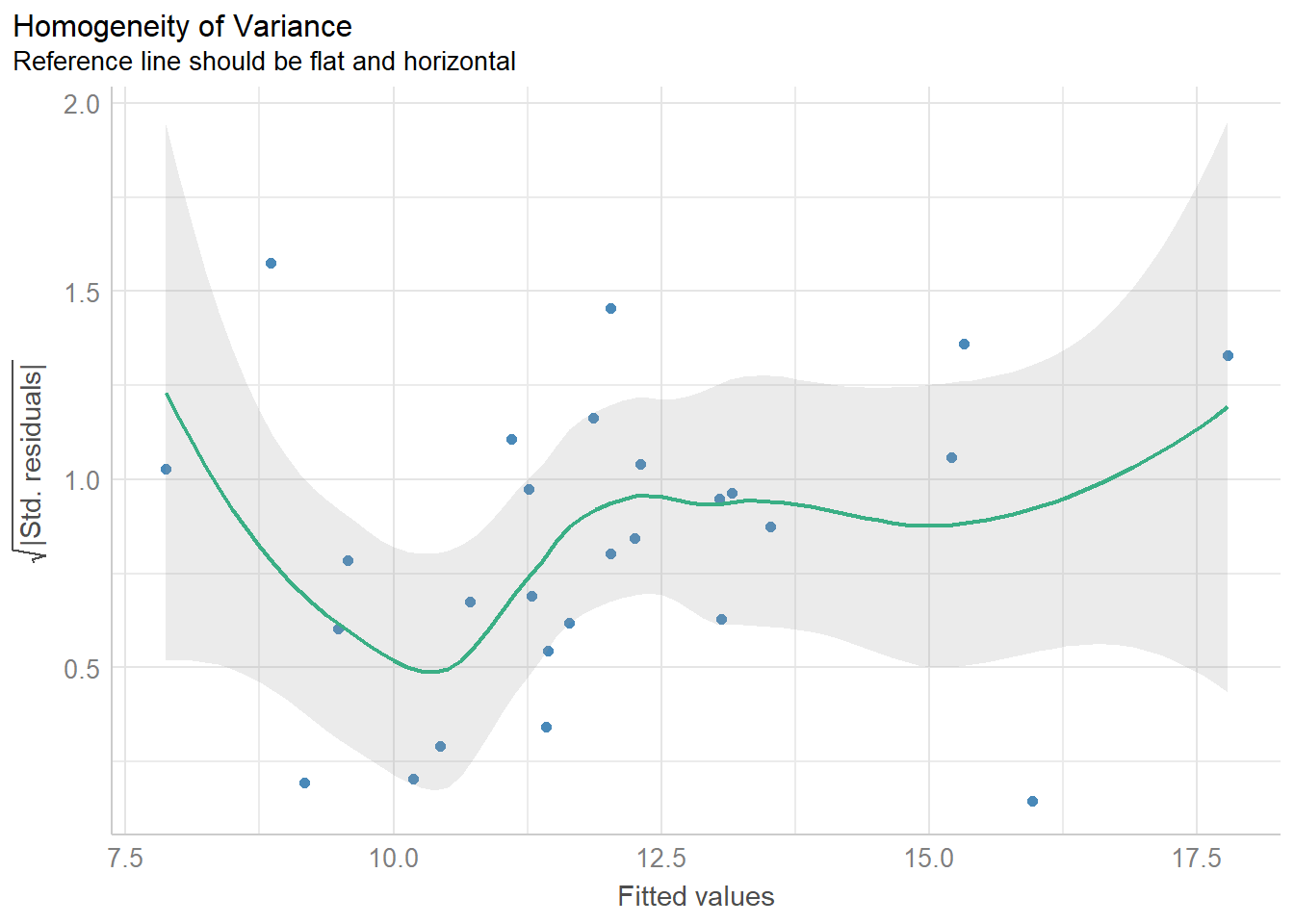

第4幅图是用来观察强影响点或者离群值、异常值的。使用的是库克距离（cook’s distance）来计算的，图中在虚线（库克距离）外的点可被认为是异常值。

diagnostic_plots[[4]]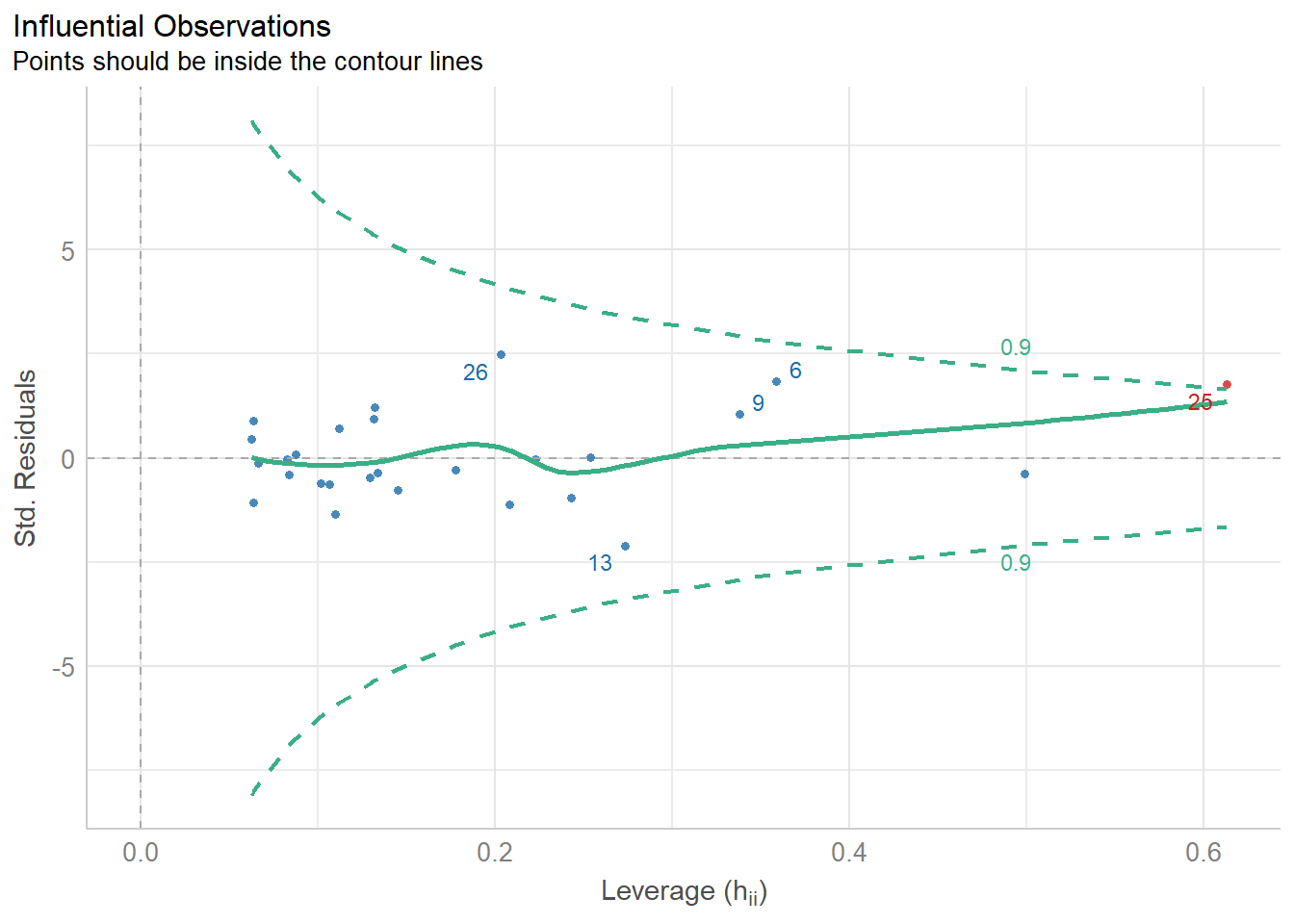

第5幅图是关于多重共线性的。是通过方差膨胀因子来评价的，下图中展示了4个变量的VIF，基本都在3以下，可认为不存在多重共线性：

diagnostic_plots[[5]]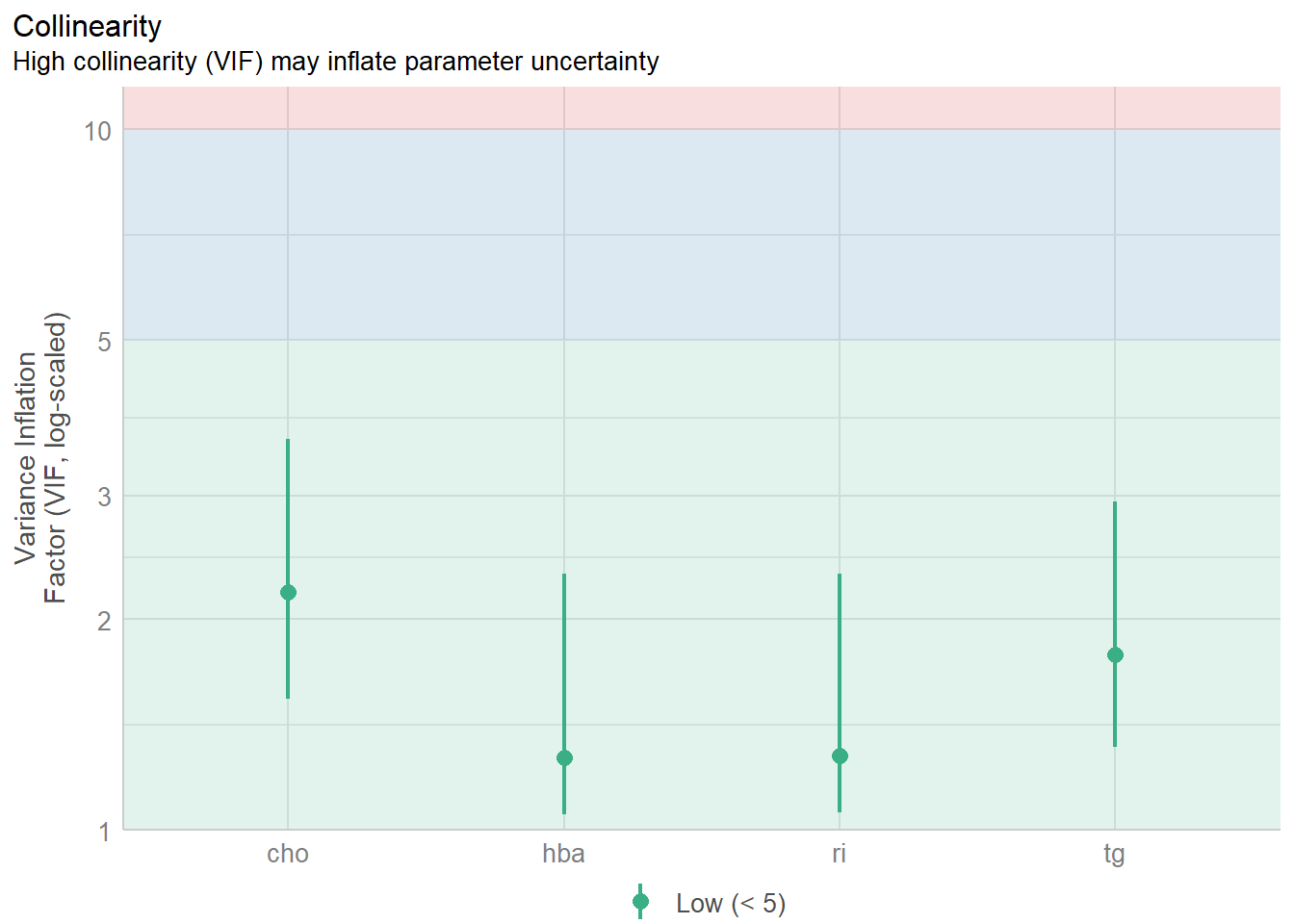

第6幅图是看正态性的。理想情况下数据点应该均匀的分布在横线上，最好是和横线重合，尤其是尾部，我们这个数据还算可以。

diagnostic_plots[[6]]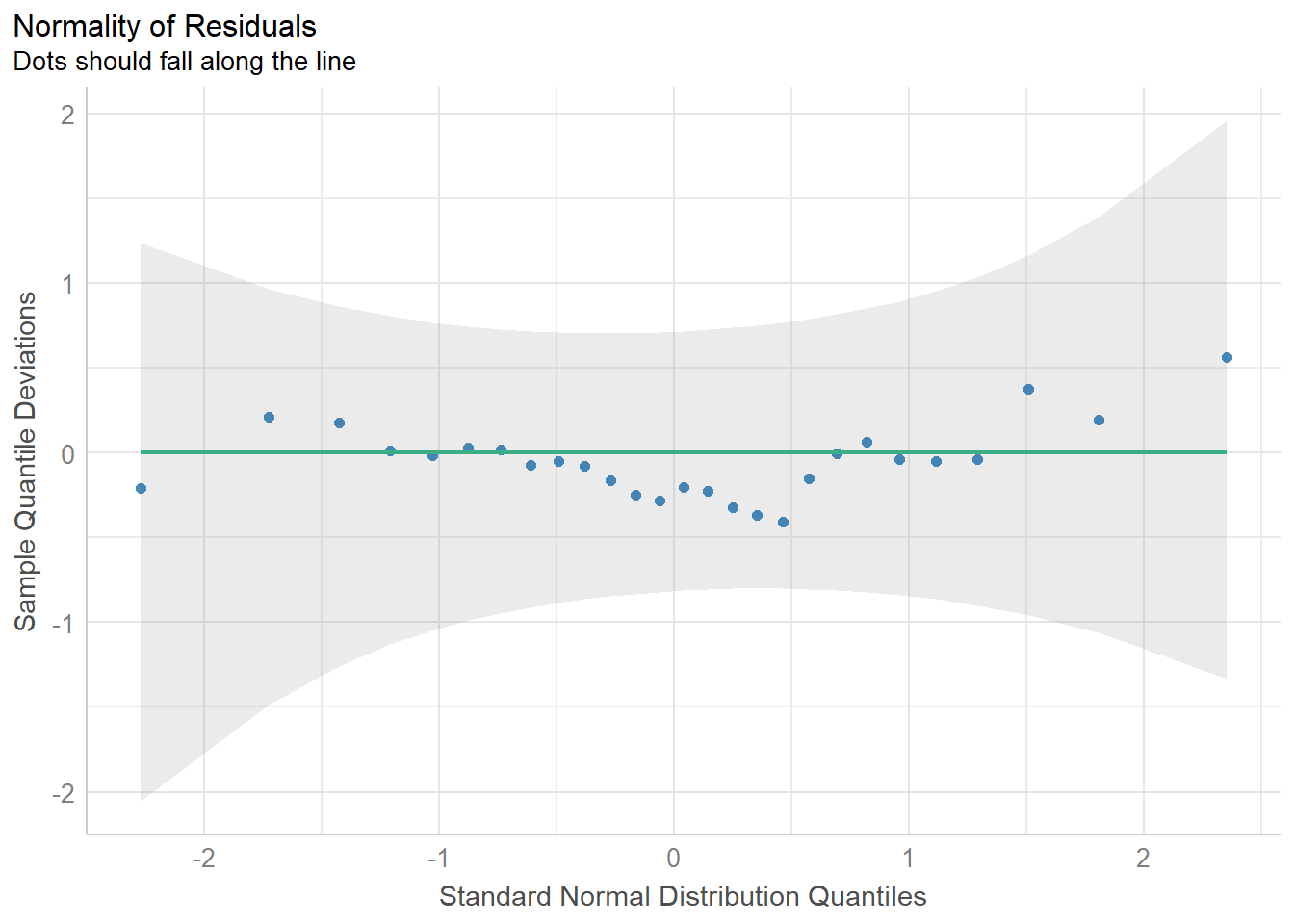

也可以通过统计方法判断，比如gvlma包可以实现对线性模型的综合判断：

library(gvlma)
gvmodel<-gvlma(f)
summary(gvmodel)
## 
## Call:
## lm(formula = fpg ~ cho + tg + ri + hba, data = df15_1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.6268 -1.2004 -0.2276  1.5389  4.4467 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)   5.9433     2.8286   2.101   0.0473 *
## cho           0.1424     0.3657   0.390   0.7006  
## tg            0.3515     0.2042   1.721   0.0993 .
## ri           -0.2706     0.1214  -2.229   0.0363 *
## hba           0.6382     0.2433   2.623   0.0155 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.01 on 22 degrees of freedom
## Multiple R-squared:  0.6008, Adjusted R-squared:  0.5282 
## F-statistic: 8.278 on 4 and 22 DF,  p-value: 0.0003121
## 
## 
## ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
## USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
## Level of Significance =  0.05 
## 
## Call:
##  gvlma(x = f) 
## 
##                      Value  p-value                   Decision
## Global Stat        9.68910 0.046003 Assumptions NOT satisfied!
## Skewness           0.65344 0.418886    Assumptions acceptable.
## Kurtosis           0.04015 0.841193    Assumptions acceptable.
## Link Function      7.68064 0.005582 Assumptions NOT satisfied!
## Heteroscedasticity 1.31487 0.251515    Assumptions acceptable.

全局统计量：粗略估计结果变量和预测变量是否符合线性关系，结果是不符合偏度和峰度：检验残差分布，结果是符合连接函数：检测结果变量是连续型还是二分类，结果是不符合异方差：检验方差齐性，结果是符合

以上是多个条件一起输出判断，也可以针对单独的条件进行判断。

首先看下正态性的判断。

library(car)
## Loading required package: carData

# 验证正态性
qqPlot(f,labels = row.names(df15_1), id.method = "identify",simulate = T,
       main = "Q-Q plot")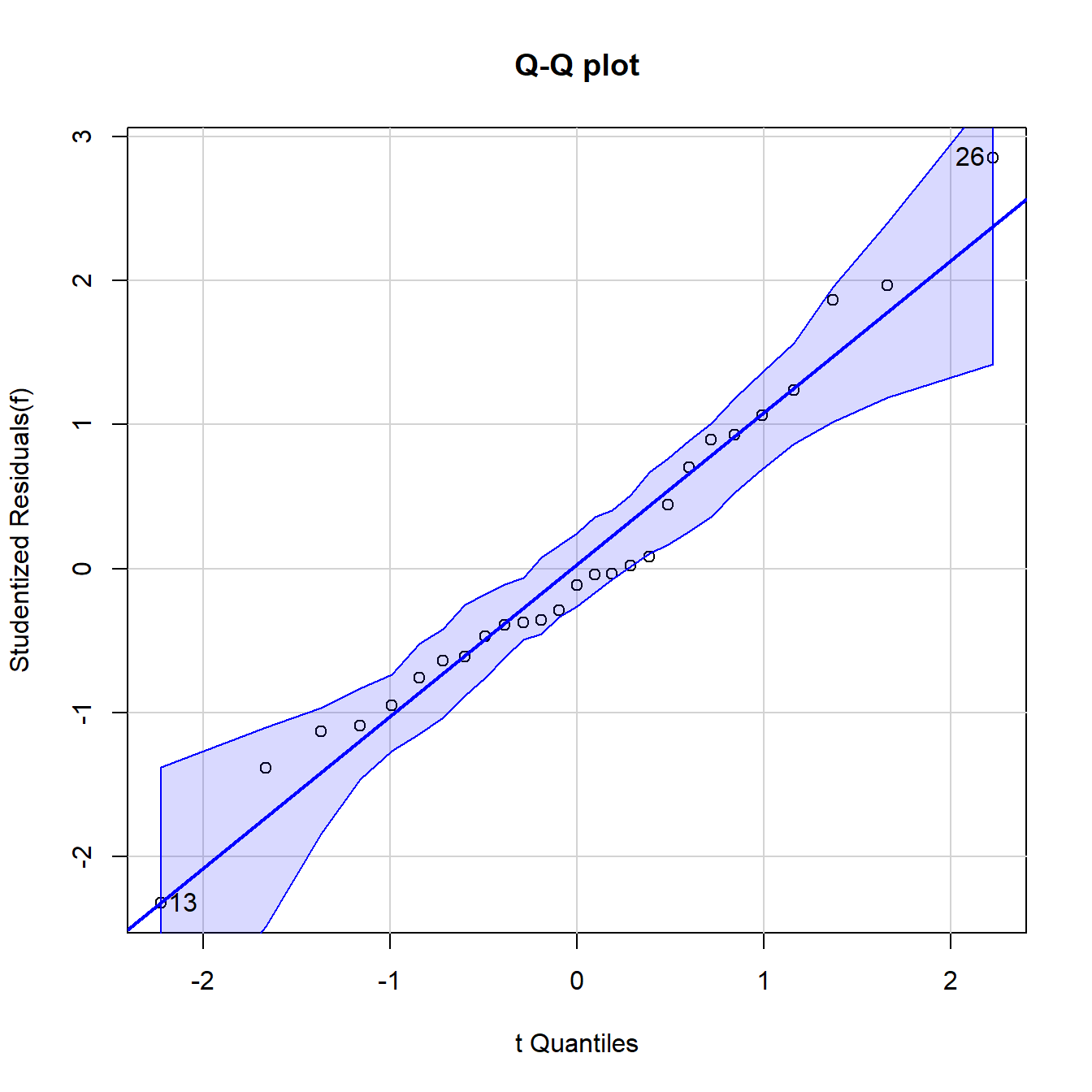

## [1] 13 26

从图中可看出正态性基本满足。

当然也可以使用非常好用的performance包实现：

check_normality(f)
## OK: residuals appear as normally distributed (p = 0.671).

检测离群值，基于cook距离：

check_outliers(f)
## 1 outlier detected: case 25.
## - Based on the following method and threshold: cook (0.9).
## - For variable: (Whole model).

检测残差（或者因变量）独立性：

set.seed(123)
check_autocorrelation(f)
## OK: Residuals appear to be independent and not autocorrelated (p = 0.296).

或者通过car包：

set.seed(123)
# 验证因变量独立性
durbinWatsonTest(f)   
##  lag Autocorrelation D-W Statistic p-value
##    1       0.1778885      1.634654   0.296
##  Alternative hypothesis: rho != 0

P值大于0.05，满足条件。

# 验证线性
crPlots(f)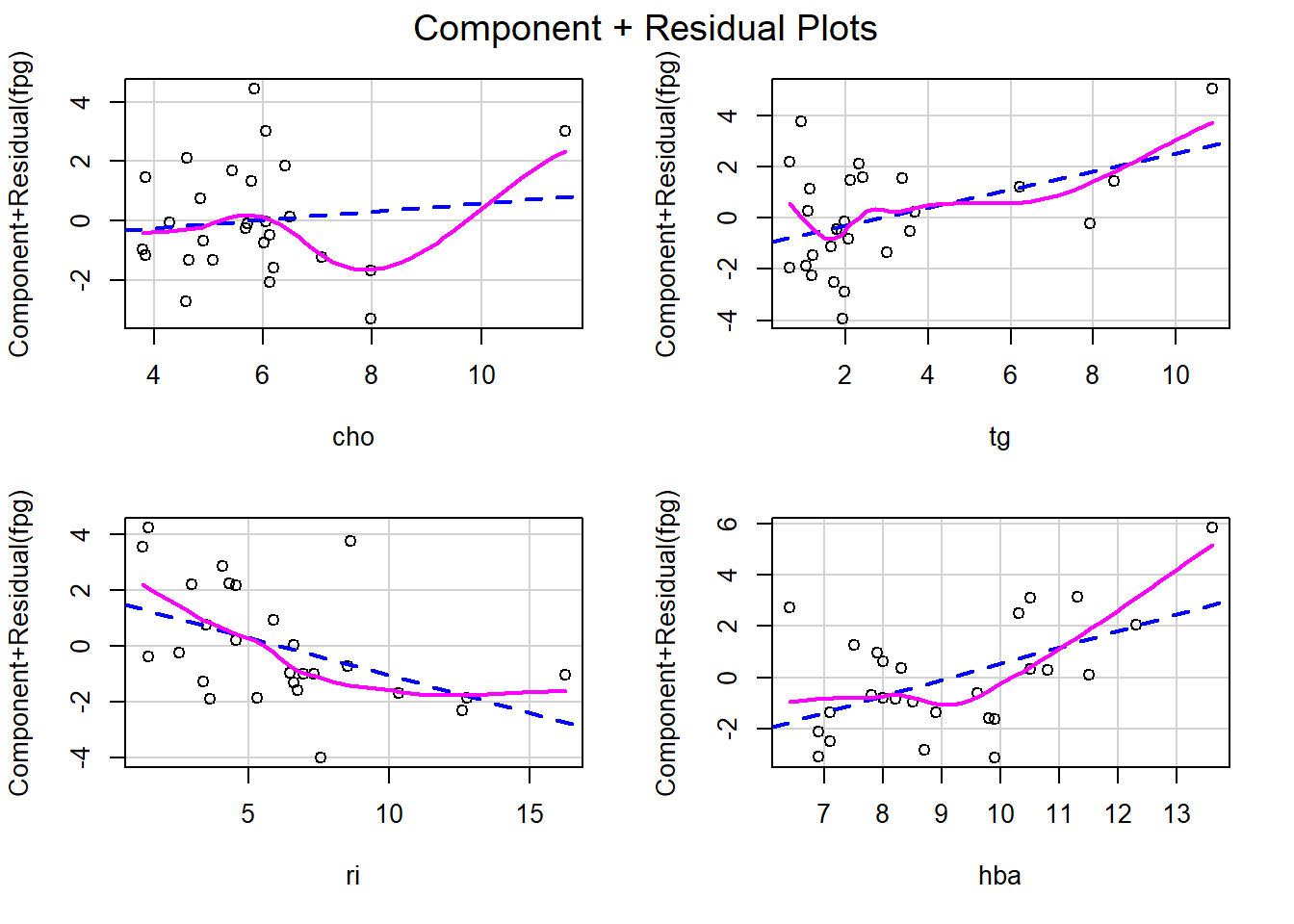

通过观察成分残差图，线性基本满足。

下面是检测方差齐性：

# 验证方差齐性
ncvTest(f)   
## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.0004274839, Df = 1, p = 0.9835

P值大于0.05，方差齐性满足。

# performance检测方差齐性
check_heteroscedasticity(f)
## OK: Error variance appears to be homoscedastic (p = 0.984).

结果一样的~

下面是多重共线性的检验，通过计算方差膨胀因子检验

vif(f)
##      cho       tg       ri      hba 
## 2.185539 1.779862 1.278364 1.266730
vif(f)>4
##   cho    tg    ri   hba 
## FALSE FALSE FALSE FALSE

都小于4（标准有争议），基本不存在多重共线性。

或者通过performance实现：

check_collinearity(f)
## # Check for Multicollinearity
## 
## Low Correlation
## 
##  Term  VIF   VIF 95% CI Increased SE Tolerance Tolerance 95% CI
##   cho 2.19 [1.54, 3.62]         1.48      0.46     [0.28, 0.65]
##    tg 1.78 [1.31, 2.95]         1.33      0.56     [0.34, 0.76]
##    ri 1.28 [1.06, 2.32]         1.13      0.78     [0.43, 0.94]
##   hba 1.27 [1.05, 2.32]         1.13      0.79     [0.43, 0.95]

11.4 参考资料

R语言实战
孙振球版医学统计学第四版
performance包官方文档