df9_1 <- data.frame(x = c(13,11,9,6,8,10,12,7),
y = c(3.54,3.01,3.09,2.48,2.56,3.36,3.18,2.65))7 双变量回归与相关
在R语言里实现非常简单。
7.1 直线回归
例9-1。
建立回归方程:
fit <- lm(y ~ x, data = df9_1)
summary(fit)
##
## Call:
## lm(formula = y ~ x, data = df9_1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.21500 -0.15937 -0.00125 0.09583 0.30667
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.66167 0.29700 5.595 0.00139 **
## x 0.13917 0.03039 4.579 0.00377 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.197 on 6 degrees of freedom
## Multiple R-squared: 0.7775, Adjusted R-squared: 0.7404
## F-statistic: 20.97 on 1 and 6 DF, p-value: 0.003774截距是1.66167,x的系数是0.13917。同时该结果也给出了回归方程的假设检验结果。
例9-2:F-statistic: 20.97,p-value: 0.003774;回归系数:t=4.579,p=0.00377。
例9-3,计算回归系数的95%的可信区间,直接使用broom计算即可:
broom::tidy(fit,conf.int = T)
## # A tibble: 2 × 7
## term estimate std.error statistic p.value conf.low conf.high
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 1.66 0.297 5.59 0.00139 0.935 2.39
## 2 x 0.139 0.0304 4.58 0.00377 0.0648 0.214例9-4,计算总体均数的可信区间和个体Y值的预测区间,1行代码即可实现:
new_x <- data.frame(x=12)
# 总体均数的可信区间
predict(fit, newdata = new_x,interval = "confidence",level = 0.95)
## fit lwr upr
## 1 3.331667 3.079481 3.583852
# 个体Y值的预测区间
predict(fit, newdata = new_x,interval = "prediction",level = 0.95)
## fit lwr upr
## 1 3.331667 2.787731 3.875602以上结果均和课本一致。
7.2 直线相关
使用课本例9-5的数据。
df <- data.frame(
weight = c(43,74,51,58,50,65,54,57,67,69,80,48,38,85,54),
kv = c(217.22,316.18,231.11,220.96,254.70,293.84,263.28,271.73,263.46,
276.53,341.15,261.00,213.20,315.12,252.08)
)
str(df)
## 'data.frame': 15 obs. of 2 variables:
## $ weight: num 43 74 51 58 50 65 54 57 67 69 ...
## $ kv : num 217 316 231 221 255 ...两变量是否有关联?其方向和密切程度如何?
直接用cor可计算相关系数r:
cor(df$weight, df$kv)
## [1] 0.8754315或者直接用cor.test,既可以计算相关系数,又可以计算相关系数的P值:
cor.test(~ weight + kv, data = df)
##
## Pearson's product-moment correlation
##
## data: weight and kv
## t = 6.5304, df = 13, p-value = 1.911e-05
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.6584522 0.9580540
## sample estimates:
## cor
## 0.8754315从结果可以看出,两者是正相关,相关系数r=0.8754,且P值小于0.05,并给出了相关系数的可信区间:(0.6584522 0.9580540),具有统计学意义!
可视化结果:
library(ggplot2)
ggplot(df, aes(weight, kv)) +
geom_point(size = 4) +
geom_smooth(method = "lm",se=F) +
geom_vline(xintercept = mean(df$weight),linetype=2)+
geom_hline(yintercept = mean(df$kv),linetype=2)+
labs(x="体重(kg)X",y="双肾体积(ml)Y")+
theme_classic()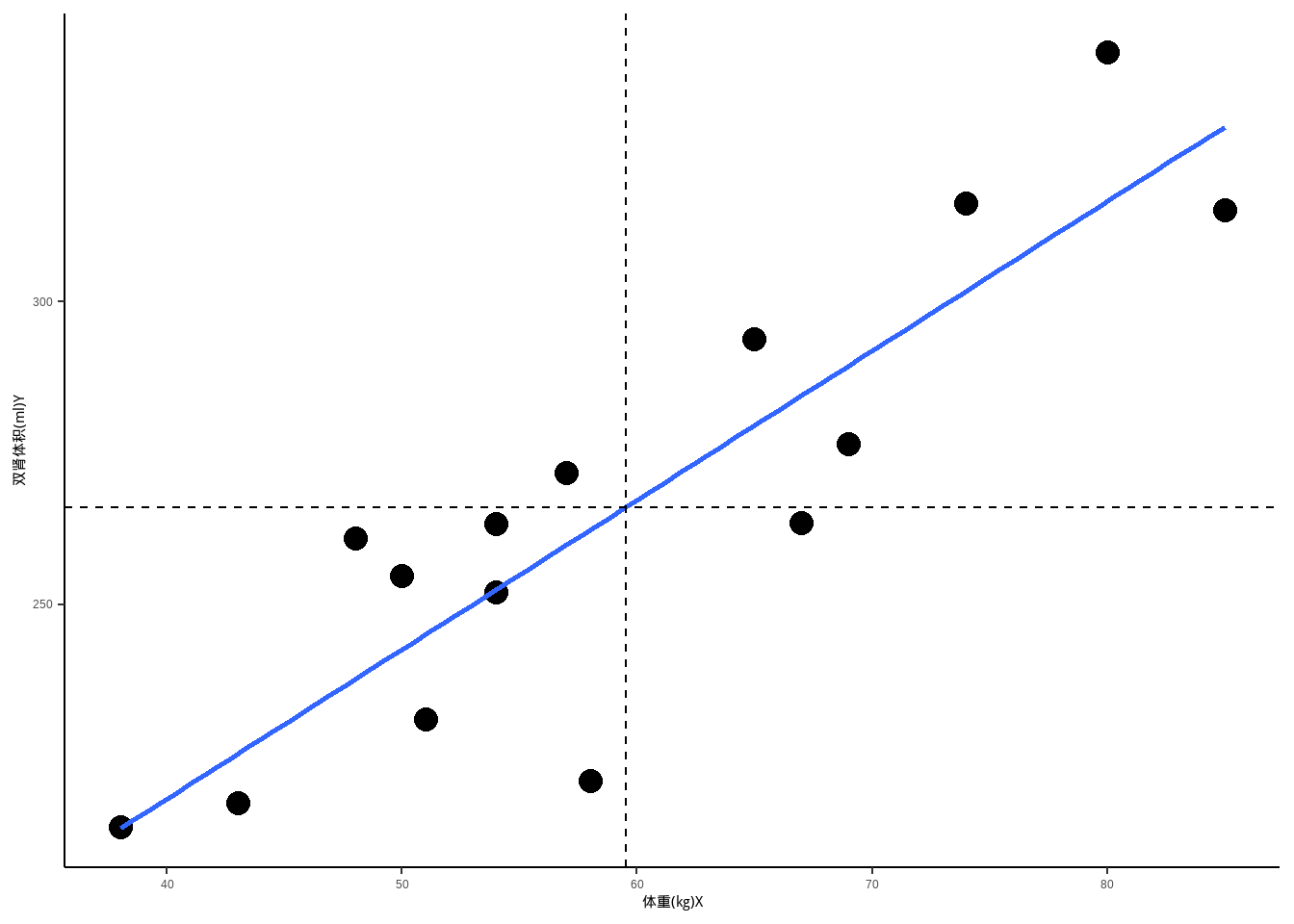
相关性分析的过程比较简单,在选择方法时要注意是使用pearson相关还是秩相关。
R2的计算:
summary(lm(weight ~ kv, data = df))
##
## Call:
## lm(formula = weight ~ kv, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.947 -4.469 -1.338 4.285 12.500
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -23.1845 12.7869 -1.813 0.093 .
## kv 0.3109 0.0476 6.530 1.91e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.777 on 13 degrees of freedom
## Multiple R-squared: 0.7664, Adjusted R-squared: 0.7484
## F-statistic: 42.65 on 1 and 13 DF, p-value: 1.911e-05Multiple R-squared: 0.7664, Adjusted R-squared: 0.7484
7.3 秩相关
例9-8
df9_8 <- foreign::read.spss("datasets/例09-08.sav", to.data.frame = T)
str(df9_8)
## 'data.frame': 18 obs. of 3 variables:
## $ number: num 1 2 3 4 5 6 7 8 9 10 ...
## $ x : num 0.03 0.14 0.2 0.43 0.44 0.45 0.47 0.65 0.95 0.96 ...
## $ y : num 0.05 0.34 0.93 0.69 0.38 0.79 1.19 4.74 2.31 5.95 ...
## - attr(*, "variable.labels")= Named chr [1:3] "\xb1\xe0\xba\xc5" "\xcb\xc0\xd2\xc9" "WYPLL\xb9\xb9\xb3\xc9"
## ..- attr(*, "names")= chr [1:3] "number" "x" "y"计算相关系数:
cor(df9_8$x,df9_8$y, method = "spearman")
## [1] 0.9050568计算P值:
cor.test(df9_8$x,df9_8$y, method = "spearman")
##
## Spearman's rank correlation rho
##
## data: df9_8$x and df9_8$y
## S = 92, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.9050568P<0.001。
如何校正?直接使用continuity即可(看帮助文档):
cor.test(df9_8$x,df9_8$y, method = "spearman",continuity=T)
##
## Spearman's rank correlation rho
##
## data: df9_8$x and df9_8$y
## S = 92, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.90505687.4 两条回归直线的比较
正常儿童数据见例9-1,大骨节病儿童数据见例9-9,问:回归直线是否不平行?
# 例9-1数据
df9_1 <- data.frame(x = c(13,11,9,6,8,10,12,7),
y = c(3.54,3.01,3.09,2.48,2.56,3.36,3.18,2.65))
# 例9-9数据
df9_9 <- foreign::read.spss("datasets/例09-09.sav", to.data.frame = T)建立回归方程:
# 例9-1的回归方程
fit9_1 <- lm(y ~ x, data = df9_1)
# 例9-2的回归方程
fit9_9 <- lm(y ~ x, data = df9_9)
a1 <- anova(fit9_1)
a1
## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## x 1 0.81343 0.81343 20.968 0.003774 **
## Residuals 6 0.23276 0.03879
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
a2 <- anova(fit9_9)
a2
## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## x 1 2.61351 2.61351 58.362 6.076e-05 ***
## Residuals 8 0.35825 0.04478
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1如果此时你直接使用anova进行F检验,会得到以下报错:
anova(fit9_1,fit9_9)
Error in anova.lmlist(object, ...) :
models were not all fitted to the same size of dataset这是因为这个函数只能处理样本量完全一样的两个模型的比较,此时我们可以把两个数据集合并到一起,添加一个交互项,查看交互项的显著性,以此来判断两条回归直线是否平行(如果有现成的函数可以比较的,请大神告诉我)。
df9_1$group <- "group9_1"
df9_9$group <- "group9_9"
df9 <- rbind(df9_1,df9_9[,-1])
df9$group <- factor(df9$group)
str(df9)
## 'data.frame': 18 obs. of 3 variables:
## $ x : num 13 11 9 6 8 10 12 7 10 9 ...
## $ y : num 3.54 3.01 3.09 2.48 2.56 3.36 3.18 2.65 3.01 2.83 ...
## $ group: Factor w/ 2 levels "group9_1","group9_9": 1 1 1 1 1 1 1 1 2 2 ...建立回归方程,并比较:
# 建立不包含交互项的模型
model_no_interaction <- lm(y ~ x + group, data = df9)
# 建立包含交互项的模型
model_interaction <- lm(y ~ x * group, data = df9)
# 使用anova函数比较两个模型
anova(model_no_interaction, model_interaction)
## Analysis of Variance Table
##
## Model 1: y ~ x + group
## Model 2: y ~ x * group
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 15 0.62211
## 2 14 0.59101 1 0.031103 0.7368 0.4052得到的P值大于0.05,还不能认为两条总体回归直线不平行。
当认为两条总体回归直线平行时,如果能进一步认为其总体截距是相等的,在两组数据的自变量取值范围接近时,便可认为两条总体回归直线基本重合,这时可合并两组样本资料,计算一个统一的回归方程。
下面我们检测其截距是否相等,可通过直接查看有交互项模型的结果:
# 查看模型摘要,检查group的显著性
summary(model_no_interaction)
##
## Call:
## lm(formula = y ~ x + group, data = df9)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.29885 -0.15905 0.01675 0.14186 0.34023
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.44893 0.18427 7.863 1.06e-06 ***
## x 0.16156 0.01785 9.049 1.83e-07 ***
## groupgroup9_9 -0.23256 0.10181 -2.284 0.0373 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2037 on 15 degrees of freedom
## Multiple R-squared: 0.8457, Adjusted R-squared: 0.8252
## F-statistic: 41.12 on 2 and 15 DF, p-value: 8.162e-07结果中的groupgroup9_9的P值小于0.05,说明其截距是有差异的,不相等的。
7.5 曲线拟合
有些情况两个变量的关系并不是直线形式的,有可能是曲线形式的,此时可以通过曲线拟合来刻画两变量之间的关系。主要方法就是对变量做转换,比如log、平方、多项式、样条等。
例9-11。
df9_11 <- foreign::read.spss("datasets/例09-11.sav", to.data.frame = T)
str(df9_11)
## 'data.frame': 5 obs. of 3 variables:
## $ number: num 1 2 3 4 5
## $ x : num 0.005 0.05 0.5 5 25
## $ y : num 34.1 58 94.5 128.5 170
## - attr(*, "variable.labels")= Named chr [1:3] "编号" " CRF浓度" "ACTH的合成量"
## ..- attr(*, "names")= chr [1:3] "number" "x" "y"
## - attr(*, "codepage")= int 936先画图查看趋势:
library(ggplot2)
ggplot(df9_11, aes(x,y))+
geom_point(size=4)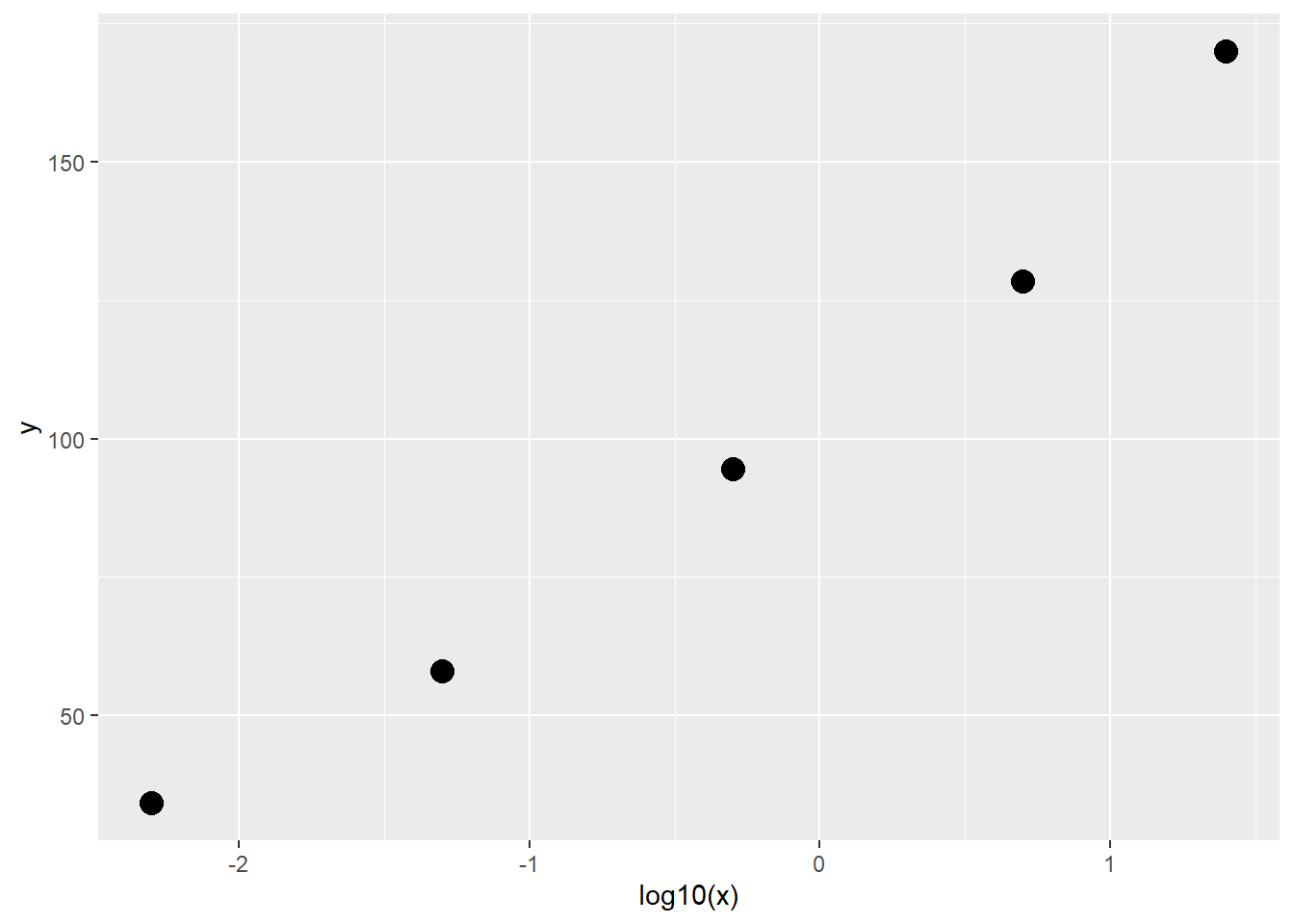
可以发现这个趋势非常像高中学过的对数函数的图像,所以我们选择对自变量X做对数转换,再画图看一看:
ggplot(df9_11, aes(log10(x),y))+
geom_point(size=4)
果然就基本上呈直线趋势了,所以我们选择对数转换后的X建立直线回归方程:
f9_11 <- lm(y ~ log10(x), data = df9_11)
summary(f9_11)
##
## Call:
## lm(formula = y ~ log10(x), data = df9_11)
##
## Residuals:
## 1 2 3 4 5
## 7.152 -5.083 -4.698 -6.804 9.433
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 110.060 4.095 26.88 0.000113 ***
## log10(x) 36.115 2.968 12.17 0.001195 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.838 on 3 degrees of freedom
## Multiple R-squared: 0.9801, Adjusted R-squared: 0.9735
## F-statistic: 148.1 on 1 and 3 DF, p-value: 0.001195例9-12。
df9_12 <- foreign::read.spss("datasets/例09-12.sav", to.data.frame = T)
str(df9_12)
## 'data.frame': 15 obs. of 2 variables:
## $ x: num 2 5 7 10 14 19 26 31 34 38 ...
## $ y: num 54 50 45 37 35 25 20 16 18 13 ...
## - attr(*, "variable.labels")= Named chr [1:2] "סԺ\xcc\xec\xca\xfd" "Ԥ\xba\xf3ָ\xca\xfd"
## ..- attr(*, "names")= chr [1:2] "x" "y"先画图看趋势:
ggplot(df9_12, aes(x,y))+
geom_point(size=4)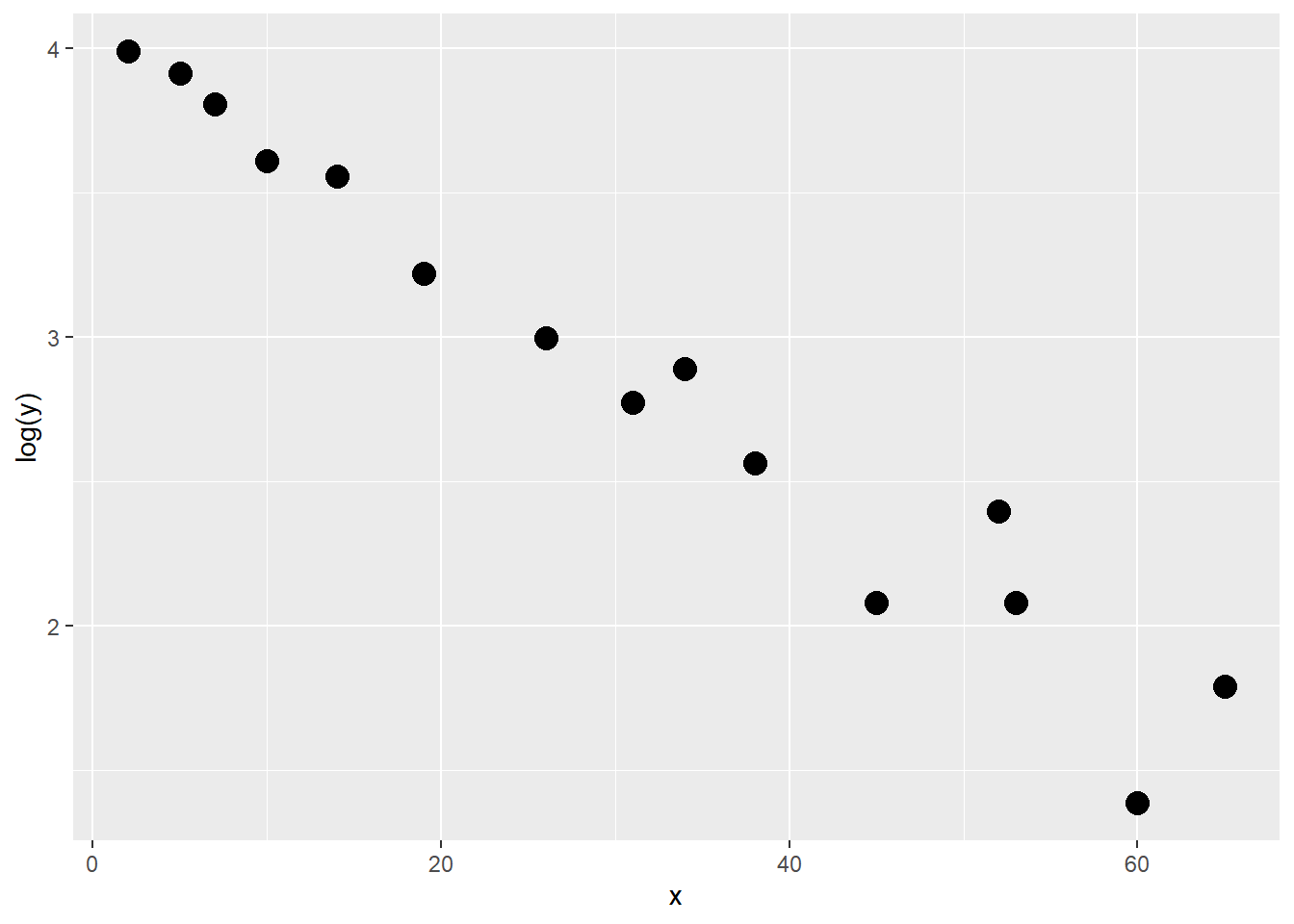
这个图有点像指数函数的图像,我们可以尝试对因变量Y做对数转换,再画图看看:
ggplot(df9_12, aes(x,log(y)))+
geom_point(size=4)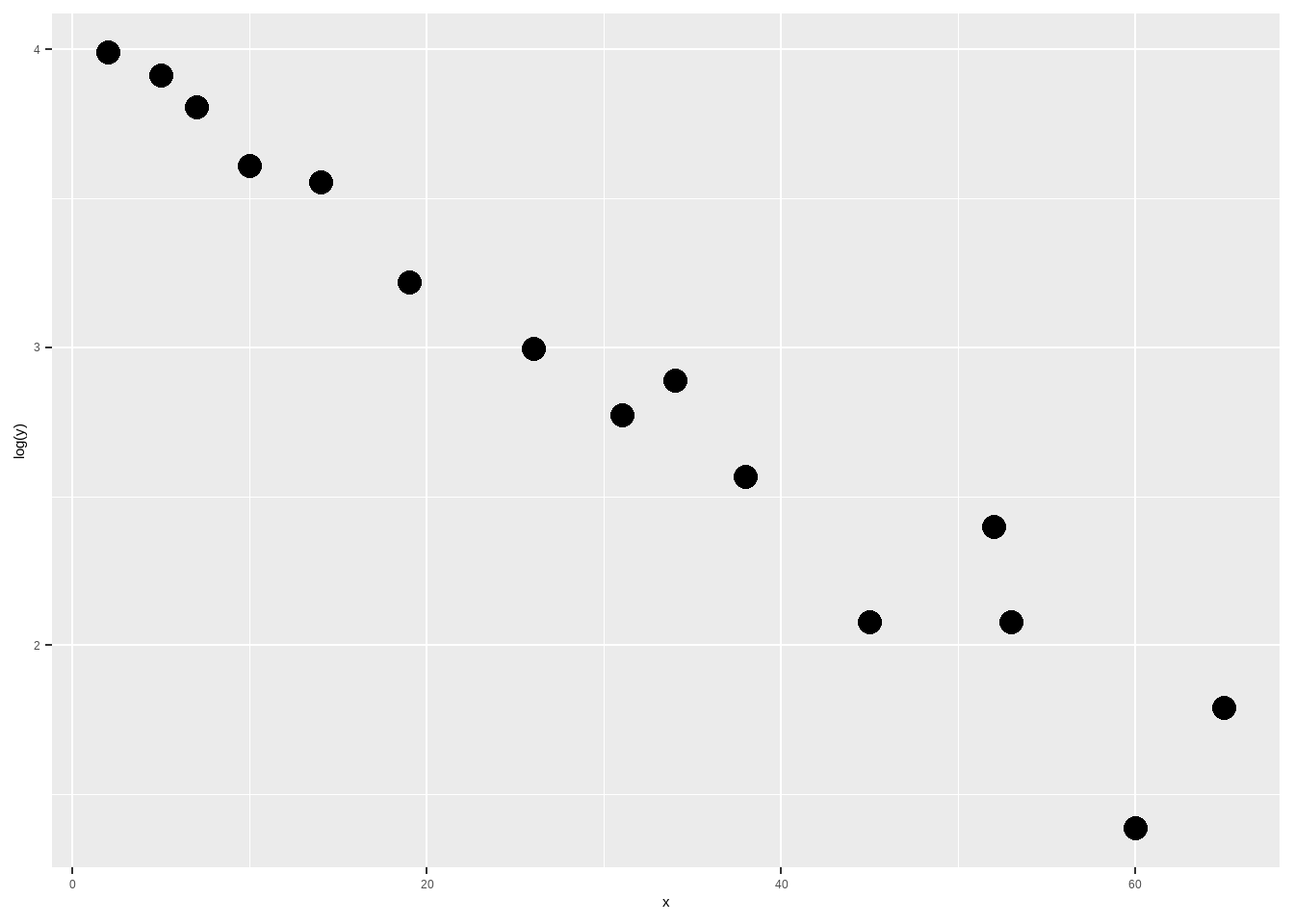
果然就基本上呈直线趋势了,所以我们选择对数转换后的Y建立直线回归方程:
f9_12 <- lm(log(y) ~ x, data = df9_12)
summary(f9_12)
##
## Call:
## lm(formula = log(y) ~ x, data = df9_12)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.37241 -0.07073 0.02777 0.05982 0.33539
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.037159 0.084103 48.00 5.08e-16 ***
## x -0.037974 0.002284 -16.62 3.86e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1794 on 13 degrees of freedom
## Multiple R-squared: 0.9551, Adjusted R-squared: 0.9516
## F-statistic: 276.4 on 1 and 13 DF, p-value: 3.858e-10