29 R语言倾向性评分：回归和分层

倾向性评分有4种应用，前面介绍了倾向性评分匹配及matchIt和cobalt包的使用。

今天说一下倾向性评分回归和分层。使用了一个不是很成功的案例，并使用了大量purrr风格的代码实现。

29.1 演示数据

下面这个例子探讨不同学校对学生成绩的影响，这个数据一共有11078行，23列，我们只用其中一部分数据演示倾向性评分回归和分层。

我们用到以下几个变量：

catholic：是我们的处理因素，1是天主教（catholic）学校，0是公立（public）学校，
c5r2mtsc_std：结果变量（因变量），标准化之后的学生成绩，
race_white：是否是白人，1是0否，
w3momed_hsb：妈妈的教育水平，1高中及以下，0大学及以上，
p5hmage：妈妈的年龄，要控制的混杂因素，
w3momscr：妈妈的成绩，
w3dadscr：爸爸的成绩。

首先加载数据，已上传到QQ群，需要的加群下载即可。

library(tidyverse)

ecls <- read.csv("datasets/ecls.csv") %>% 
  dplyr::select(c5r2mtsc_std,catholic,race_white,w3momed_hsb,p5hmage,
                w3momscr,w3dadscr) %>%
  na.omit()

dim(ecls)
## [1] 5548    7
glimpse(ecls)
## Rows: 5,548
## Columns: 7
## $ c5r2mtsc_std <dbl> 0.98175332, 0.59437751, 0.49061062, 1.45127793, 2.5956991…
## $ catholic     <int> 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ race_white   <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, …
## $ w3momed_hsb  <int> 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, …
## $ p5hmage      <int> 47, 41, 43, 38, 47, 41, 31, 38, 26, 38, 27, 40, 33, 36, 4…
## $ w3momscr     <dbl> 53.50, 34.95, 63.43, 53.50, 61.56, 38.18, 34.95, 63.43, 3…
## $ w3dadscr     <dbl> 77.50, 53.50, 53.50, 53.50, 77.50, 53.50, 29.60, 33.42, 2…

29.2 原始数据的概况

首先看一下原始数据的情况。

ecls %>%
  group_by(catholic) %>%
  summarise(n_students = n(),
            mean_math = mean(c5r2mtsc_std),
            std_error = sd(c5r2mtsc_std) / sqrt(n_students))
## # A tibble: 2 × 4
##   catholic n_students mean_math std_error
##      <int>      <int>     <dbl>     <dbl>
## 1        0       4597     0.156    0.0144
## 2        1        951     0.221    0.0277

可以看到去公立学校的4597人，去天主教学校的才951人，并且去天主教的学校的学生成绩明显高于去公立学校的学生。

此时如果不控制混杂因素直接进行t检验，结果是有统计学意义的，但是由于基线资料不可比，一开始两组学生的各种情况就不一样，所以结果很难说明成绩不同到底是不同学校导致的还是混杂因素导致的。

with(ecls, t.test(c5r2mtsc_std ~ catholic))
## 
##  Welch Two Sample t-test
## 
## data:  c5r2mtsc_std by catholic
## t = -2.0757, df = 1508.1, p-value = 0.03809
## alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
## 95 percent confidence interval:
##  -0.126029105 -0.003564746
## sample estimates:
## mean in group 0 mean in group 1 
##       0.1562757       0.2210727

我们可以看看不同组别间混杂因素的差异，首先是3个连续型变量在两组间的平均值，可以看到都是不一样的：

ecls %>%
  group_by(catholic) %>%
  select(p5hmage, w3momscr, w3dadscr) %>%
  summarise_all(list(~mean(., na.rm = T)))
## # A tibble: 2 × 4
##   catholic p5hmage w3momscr w3dadscr
##      <int>   <dbl>    <dbl>    <dbl>
## 1        0    37.8     43.8     42.6
## 2        1    39.8     47.5     45.8

可以看到不同组别间混杂因素明显是不同的，还可以分别对3个连续型变量做t检验，结果也显示这些混杂因素在一开始就是存在差异的。

ecls %>% 
  pivot_longer(cols = c(p5hmage,w3momscr,w3dadscr),
               names_to = "covs",
               values_to = "values"
               ) %>% 
  group_split(covs) %>% 
  map(~t.test(values ~ catholic, data = .x)) %>% 
  map_dbl("p.value")
## [1] 1.062659e-28 3.722314e-16 2.208513e-18

对于两个分类变量，我们可以看看分别在两组间的数量构成比有没有差异。

tab <- xtabs(~race_white+catholic,data = ecls)
tab
##           catholic
## race_white    0    1
##          0 1610  222
##          1 2987  729
chisq.test(tab,correct = F)
## 
##  Pearson's Chi-squared test
## 
## data:  tab
## X-squared = 48.596, df = 1, p-value = 3.145e-12

tab <- xtabs(~w3momed_hsb+catholic,data = ecls)
tab
##            catholic
## w3momed_hsb    0    1
##           0 2777  751
##           1 1820  200
chisq.test(tab,correct = F)
## 
##  Pearson's Chi-squared test
## 
## data:  tab
## X-squared = 117.24, df = 1, p-value < 2.2e-16

可以看到两个分类变量在两组间的差异是非常明显的！

所以我们现在要做的事就是控制混杂因素，让这些混杂因素变成可比的状态，不要影响我们的处理因素。

开头也说过，控制混杂因素的方法其实是很多的，比如分层、协方差分析、多因素分析等，每种情况都要具体分析，选择一种最合适的。

下面我们介绍倾向性评分回归和分层。

29.3 计算倾向性评分

倾向性评分就是倾向干预的概率，所以可以通过逻辑回归计算P值，这个P值就是倾向性评分，所以也不一定要用到专用的R包！

首先以处理因素（这里是catholic）为因变量，混杂因素为自变量构建逻辑回归模型：

m_ps <- glm(catholic ~ race_white+w3momed_hsb+p5hmage+w3momscr+w3dadscr,
            family = binomial(), data = ecls)

提取P值，也就是倾向性评分：

prs_df <- data.frame(pr_score = predict(m_ps, type = "response"),
                     catholic = m_ps$model$catholic)
head(prs_df)
##    pr_score catholic
## 1 0.3755223        0
## 2 0.2340976        0
## 4 0.2990706        0
## 5 0.2394663        1
## 6 0.3920115        0
## 8 0.2391453        0

可以看一下不同处理因素间的P值（倾向性评分）分布：

labs <- paste("Actual school type attended:", c("Catholic", "Public"))
prs_df %>%
  mutate(catholic = ifelse(catholic == 1, labs[1], labs[2])) %>%
  ggplot(aes(x = pr_score)) +
  geom_histogram(color = "white") +
  facet_wrap(~catholic) +
  xlab("Probability of going to Catholic school") +
  theme_bw()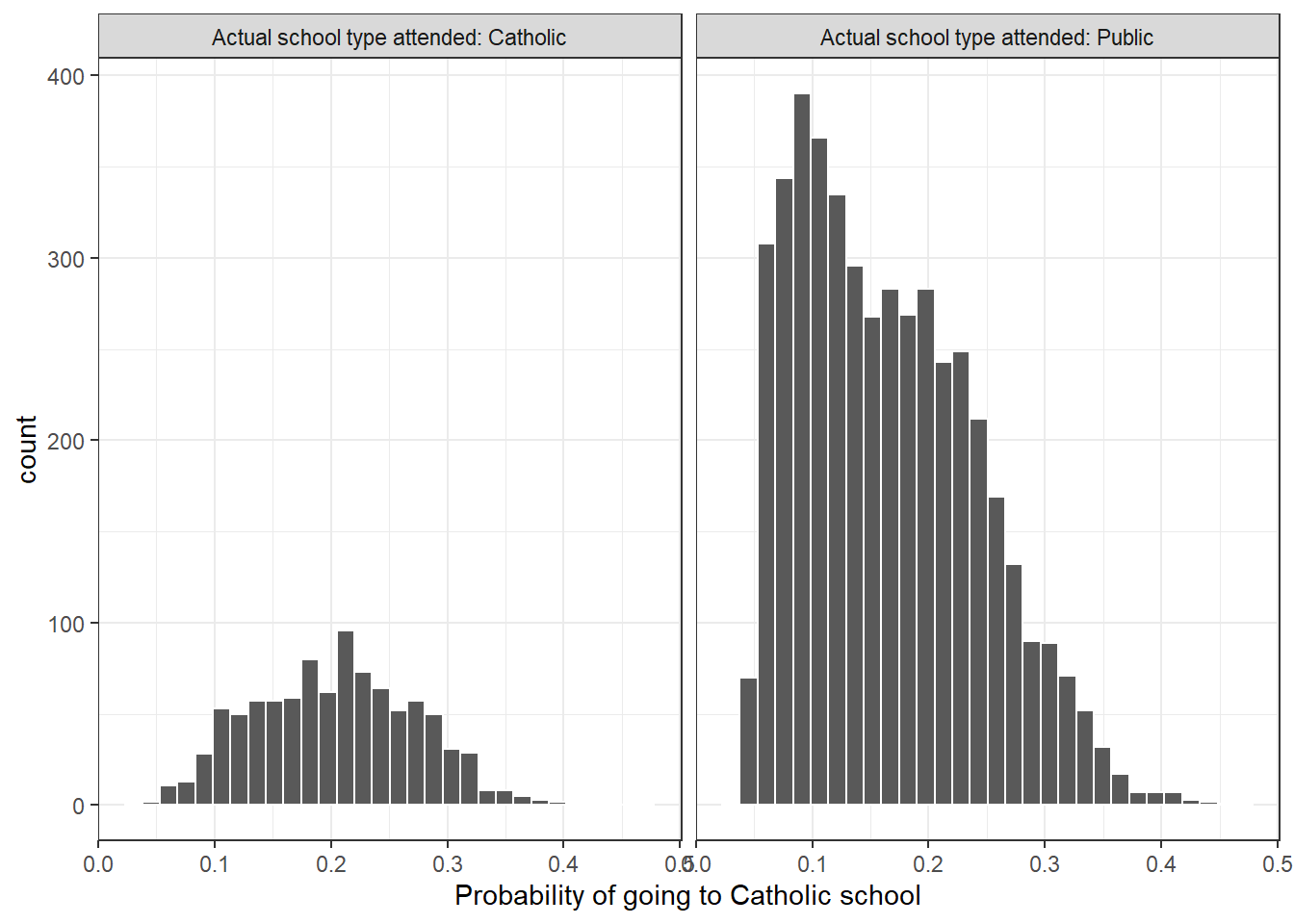

计算倾向性评分只是第一步，有了这个倾向性评分后，就可以进行下面的分析了，比如回归、匹配、加权、分层等。

可以看出我们这个PS是偏态的，其实是可以对PS做一些变换的，比如log，然后使用变换后的PS继续进行后面的分析。这里就不做变换了。

29.4 倾向性评分回归

此时如果直接把这个评分和catholic作为自变量进行回归分析，就是倾向性评分回归了（也叫协变量调整/倾向性评分矫正等）！应该是倾向性评分4种方法里面最简单的一种了。

# 计算倾向性评分
pr_score <- predict(m_ps, type = "response")

# 把倾向性评分加入到原数据中
ecls_ps <- ecls %>% 
  mutate(ps = pr_score)

# 把处理因素和倾向性评分作为自变量进行回归
psl <- lm(c5r2mtsc_std ~ catholic + ps, data = ecls_ps)
summary(psl)
## 
## Call:
## lm(formula = c5r2mtsc_std ~ catholic + ps, data = ecls_ps)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.0525 -0.5741  0.0462  0.6106  3.1468 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.58249    0.02929 -19.885  < 2e-16 ***
## catholic    -0.10772    0.03241  -3.324 0.000893 ***
## ps           4.48236    0.15873  28.239  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8934 on 5545 degrees of freedom
## Multiple R-squared:  0.1263, Adjusted R-squared:  0.126 
## F-statistic: 400.8 on 2 and 5545 DF,  p-value: < 2.2e-16

结果表明处理因素(分组变量)还是有意义的！

29.5 倾向性评分分层

顾名思义，根据PS值进行分层，然后在每层内进行分析。每一层的协变量分布可认为是同质或均衡的。先对每一层干预与结局之间的关联进行估算，然后对所有层的关联作加权平均，最后得出干预与结局之间的总的关联效应。

一般来说最好保证干预组和对照组两组的PS范围在差不多的范围内，如果相差很大，那分层效果肯定不好。比如干预组PS范围是0.5_{0.9，对照组PS范围是0.01}0.4，这样两组PS完全没有交集，按照PS进行分层没啥意义。

首先看一下PS的范围：

ecls_ps %>% group_by(catholic) %>% 
  summarise(range = range(ps))
## Warning: Returning more (or less) than 1 row per `summarise()` group was deprecated in
## dplyr 1.1.0.
## ℹ Please use `reframe()` instead.
## ℹ When switching from `summarise()` to `reframe()`, remember that `reframe()`
##   always returns an ungrouped data frame and adjust accordingly.
## # A tibble: 4 × 2
## # Groups:   catholic [2]
##   catholic  range
##      <int>  <dbl>
## 1        0 0.0370
## 2        0 0.477 
## 3        1 0.0492
## 4        1 0.404

两组分别是0.037_{0.477和0.049}0.404，范围基本一致，所以我们就直接按照总体PS的最大值和最小值进行分层，如果两组PS差很多，可以按照两组PS的交集进行分层。

文献一般建议分5-10层，可以根据PS进行平分，也可以按照百分位数进行分层，具体方法很多，大家自己看文献即可。

我们这里简单点，结合上面PS的分布图，分4层，切点就用0.1,0.2,0.3。

ecls_pslevel <- ecls_ps %>% 
  mutate(ps_level = case_when(ps<=0.1 ~ "level_1",
                              ps>0.1 & ps<=0.2 ~ "level_2",
                              ps>0.2 & ps<=0.3 ~ "level_3",
                              TRUE ~ "level_4"
                              ),
         #ps_level = factor(ps_level),
         p5hmage = as.double(p5hmage),
         across(where(is.integer), as.factor)
         )

glimpse(ecls_pslevel)
## Rows: 5,548
## Columns: 9
## $ c5r2mtsc_std <dbl> 0.98175332, 0.59437751, 0.49061062, 1.45127793, 2.5956991…
## $ catholic     <fct> 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ race_white   <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, …
## $ w3momed_hsb  <fct> 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, …
## $ p5hmage      <dbl> 47, 41, 43, 38, 47, 41, 31, 38, 26, 38, 27, 40, 33, 36, 4…
## $ w3momscr     <dbl> 53.50, 34.95, 63.43, 53.50, 61.56, 38.18, 34.95, 63.43, 3…
## $ w3dadscr     <dbl> 77.50, 53.50, 53.50, 53.50, 77.50, 53.50, 29.60, 33.42, 2…
## $ ps           <dbl> 0.37552233, 0.23409764, 0.29907061, 0.23946627, 0.3920115…
## $ ps_level     <chr> "level_4", "level_3", "level_3", "level_3", "level_4", "l…

29.6 分层后的数据

下面我们对每一层内的3个连续型协变量和我们的因变量进行t检验，其实这里可以直接用rstatix包解决，非常好用，但其实rstatix包就是基于purrr的，所以直接用purrr也可以。

ecls_pslevel %>% 
  pivot_longer(cols = c(1,5:7),names_to = "variates",values_to = "values") %>% 
  group_nest(ps_level,variates) %>% 
  dplyr::mutate(tt = map(data, ~ t.test(values ~ catholic,data = .x)),
                res = map_dfr(tt, broom::tidy)
                ) %>% 
  unnest(res)
## # A tibble: 16 × 14
##    ps_level variates         data tt      estimate estimate1 estimate2 statistic
##    <chr>    <chr>     <list<tibb> <list>     <dbl>     <dbl>     <dbl>     <dbl>
##  1 level_1  c5r2mtsc… [1,202 × 5] <htest> -0.00108    -0.347   -0.346   -0.00973
##  2 level_1  p5hmage   [1,202 × 5] <htest> -1.00       32.9     33.9     -1.66   
##  3 level_1  w3dadscr  [1,202 × 5] <htest> -0.639      36.8     37.4     -0.886  
##  4 level_1  w3momscr  [1,202 × 5] <htest> -1.07       37.0     38.1     -1.40   
##  5 level_2  c5r2mtsc… [2,388 × 5] <htest>  0.0685      0.142    0.0737   1.54   
##  6 level_2  p5hmage   [2,388 × 5] <htest> -0.724      37.4     38.1     -2.92   
##  7 level_2  w3dadscr  [2,388 × 5] <htest> -0.818      40.7     41.5     -1.73   
##  8 level_2  w3momscr  [2,388 × 5] <htest> -1.13       41.3     42.5     -2.21   
##  9 level_3  c5r2mtsc… [1,618 × 5] <htest>  0.171       0.533    0.361    3.46   
## 10 level_3  p5hmage   [1,618 × 5] <htest>  0.00290    41.1     41.1      0.0141 
## 11 level_3  w3dadscr  [1,618 × 5] <htest> -1.36       47.5     48.8     -2.17   
## 12 level_3  w3momscr  [1,618 × 5] <htest> -0.371      50.9     51.3     -0.573  
## 13 level_4  c5r2mtsc…   [340 × 5] <htest>  0.0580      0.728    0.670    0.548  
## 14 level_4  p5hmage     [340 × 5] <htest>  0.820      46.2     45.4      1.84   
## 15 level_4  w3dadscr    [340 × 5] <htest>  0.868      59.6     58.7      0.582  
## 16 level_4  w3momscr    [340 × 5] <htest> -0.739      60.0     60.7     -0.637  
## # ℹ 6 more variables: p.value <dbl>, parameter <dbl>, conf.low <dbl>,
## #   conf.high <dbl>, method <chr>, alternative <chr>

直接看p.value这一列，可以看到大部分都是大于0.05的，因变量c5r2mtsc_std只有在第3层是有差异的！

level_2中的p5hmage和w3momscr变量的P值是小于0.05的，level_3中的w3dadscr变量P值也是小于0.05的。

这说明我们的分层并没有很好的解决这几个混杂因素的影响，而且分层后每一层内（除了第3层）的因变量都没有差异了。。。理想的结果应该是分层后每一层内混杂因素在两组间都是没有差异的，而因变量都是有差异的！这样才能说明我们的分层很好地控制了混杂因素！

但我们的这个结果很明显很差劲！大家可以考虑不同的分层方法再重新尝试几次，或者这个数据并不适合使用这种方法，可以用其他方法试试看，比如匹配、回归等。

下面再看看分类变量，首先是race_white，在每一层内使用卡方检验，我们直接提取P值：

ecls_pslevel %>% 
  group_split(ps_level) %>% 
  map(~chisq.test(.$race_white,.$catholic,correct=F)) %>% 
  map_dbl("p.value")
## Warning in chisq.test(.$race_white, .$catholic, correct = F): Chi-squared
## approximation may be incorrect
## [1] 0.4755703 0.8423902 0.5696924 0.2667193

结果还不错，每一层内都没有差异了。

然后是w3momed_hsb这个变量，但是由于我们的分层有问题，导致level_4这一层中w3momed_hsb全都是0！

# level_4有问题
ecls_pslevel %>% 
  group_by(ps_level,w3momed_hsb,catholic) %>% 
  summarise(count=n())
## # A tibble: 14 × 4
## # Groups:   ps_level, w3momed_hsb [7]
##    ps_level w3momed_hsb catholic count
##    <chr>    <fct>       <fct>    <int>
##  1 level_1  0           0           61
##  2 level_1  0           1            5
##  3 level_1  1           0         1082
##  4 level_1  1           1           54
##  5 level_2  0           0         1262
##  6 level_2  0           1          261
##  7 level_2  1           0          724
##  8 level_2  1           1          141
##  9 level_3  0           0         1192
## 10 level_3  0           1          407
## 11 level_3  1           0           14
## 12 level_3  1           1            5
## 13 level_4  0           0          262
## 14 level_4  0           1           78

所以我们就对前3层做一个统计检验吧。

ecls_pslevel %>% 
  filter(!ps_level == "level_4") %>% 
  group_split(ps_level) %>% 
  map(~chisq.test(.$w3momed_hsb,.$catholic,correct=F)) %>% 
  map_dbl("p.value")
## Warning in chisq.test(.$w3momed_hsb, .$catholic, correct = F): Chi-squared
## approximation may be incorrect
## Warning in chisq.test(.$w3momed_hsb, .$catholic, correct = F): Chi-squared
## approximation may be incorrect
## [1] 0.3022080 0.5994507 0.9316443

可以看到每一层内也是没有明显差别的。

说明我们的分层对2个分类变量的平衡效果还是可以的，但是对连续型变量的效果真是一言难尽！

29.7 总结

倾向性评分回归和分层的大致过程就是这样的，但其实很多细节我都忽略了，比如到底分几层？依据是什么？用PS还是log(PS)？

而且特地找了一个不是很成功的例子（可能不是很恰当），结果并不是很完美，还有很多可以调整测试的空间，大家可以适当修改其中的方法细节，最后得到一个笔记好的结果。

实际使用时大家要根据自己的实际情况选择最合适的方法，多读文献，从文献中找灵感。

29.8 参考资料

https://sejdemyr.github.io/r-tutorials/statistics/tutorial8.html