26  ROC曲线

本章内容对应课本第37章第7节：临床诊断实验与评价

ROC（Receiver operating characteristic curve，ROC）曲线首先是由二战中的电子工程师和雷达工程师发明的，用来侦测战场上的敌军载具（飞机、船舰），也就是信号检测理论。之后很快就被引入了心理学来进行信号的知觉检测。数十年来，ROC分析被用于医学、无线电、生物学、犯罪心理学领域中，而且在机器学习（machine learning）和数据挖掘（data mining）领域也得到了很好的发展。

ROC曲线在临床中主要是用来评价诊断试验的，由于ROC曲线和临床诊断试验的联系超级紧密，所以我们有必要先了解一下诊断试验相关的内容。

26.1 诊断试验

科学地评价诊断试验是临床医师选择诊断试验的基础。诊断试验在临床上的应用涉及面甚广，包括病因和病原学诊断，疾病病理和功能损害的诊断，疗效的判断，药物毒副作用的监测，疾病预后的判断以及应用于普查、筛检无症状的患者等。用于不同场合的诊断试验有不同的要求，不同的诊断试验本身又有一定的特性。为了合理选用诊断试验以避免盲目性，临床医师就需要对诊断试验进行科学研究并得出科学的评价。

评价诊断试验的优劣必须以金标准（gold standard）作为参照，没有金标准的诊断试验评价是没有科学性的。所谓诊断试验的金标准，是指当前临床医学界所公认的诊断某病最为可靠的方法。亦即利用金标准能正确地区分某人属”有病”还是”无病”。临床诊断中常用的金标准包括病理学诊断（组织活检和尸检）、外科手术发现、特殊的影像学诊断（如用冠状动脉造影术诊断冠心病等）以及目前尚无特异诊断方法而采用的国际公认的综合诊断标准（如诊断风湿热的Johes标准等）。有时用长期临床随访所获得的肯定诊断，也可作为金标准。必须注意，如果采用的金标准选择不当，就会造成分类错误，从而影响诊断试验正确性的评价。

用于诊断试验评价的研究对象应包括病例组和对照组。病例组应是按金标准确诊的患者；对照组则应是按金标准证实无该病的患者或正常人群。病例组的选择，应包括各种类型的病例，即典型和不典型，早、中、晚各期，病情轻、中、重，有、无并发症等，这样试验的结果才具有普遍意义；而对照组则可选用经金标准证实无该病的其他病例或正常人，特别应当包括确实无该病，但易与该病相混淆的其他病例，这样选择的对照才具有临床意义，尤其具有鉴别诊断的价值。

26.2 诊断试验的评价

根据诊断试验的结果和金标准的结果，可得到4种情况，将其整理成下面的表格，就得到一个诊断试验的四格表，实际上是一个配对四格表的形式：

用于评价诊断试验的常用指标有：灵敏度和特异度，误诊率和漏诊率。

• 灵敏度

灵敏度（sensitivity），又称为真阳性率，是实际患病且被试验诊断为患者的概率，即患者被诊断为阳性的概率。灵敏度=a/(a+c)

• 特异度

特异度（specificity），又被称为真阴性率，是实际未患病而被试验诊断为非患者的概率，即非患者被诊断为阴性的概率。特异度=d/(b+d)

灵敏度是反映检出能力的指标，而特异度是鉴别非患者能力的指标，二者都是越大越好。

• 误诊率

误诊率又称为假阳性率，表示实际未患病但被试验诊断为患者的概率，即非患者被诊断为阳性，反映非患者被错误诊断的可能性。误诊率=b/(b+d)

• 漏诊率

漏诊率又被称为假阳性率，表示实际患病但被试验诊断为非患者的概率，即患者被诊断为阴性，反映患者被遗漏诊断的可能性。漏诊率=c/(a+c)

显然，灵敏度=1-假阴性率，特异度=1-假阳性率。

除了以上4个指标外，还有阳性预测值和阴性预测值，用于评价诊断试验预测的准确性。

• 阳性预测值：positive-predict-value，是试验诊断为阳性者，确为患者的概率。阳性预测值=a/(a+b)。
• 阴性预测值：negative-predict-value，是试验诊断为阴性者，确为非患者的概率。阴性预测值=d/(c+d)。

当两个诊断试验进行比较时，单独使用灵敏度与特异度指标，可能出现一个诊断试验的灵敏度高，而另一个诊断试验的特异度高，无法判断哪一个更好。所以发展出了可以将灵敏度和特异度综合起来评价的诊断试验指标，比如：正确率、比数积、阳新似然比、阴性似然比等。

• 正确率：又称为准确率（机器学习中被称为accuracy），又称为总符合率，表示观察结果和实际结果的符合程度，反应正确诊断患者与非患者的能力。正确率=(a+d)/N，N是总人数。

• 约登指数：Youden-index，YI，是反应诊断试验真实性的综合指标，YI=灵敏度+特异度=1。YI的值在-1到1之间，越大说明诊断试验的真实性越好，当YI小于等于0时，该诊断试验无任何临床应用价值。

• 比数积：odd-product，OP，表示患者中诊断阳性数、阴性数之比和非患者中诊断阴性数、阳性数之比的乘积。OP=se/(1-se) * sp/(1-sp) = ad/bc。OP越大诊断价值越高。

• 阳性似然比：positive-likelihood-ratio，LR+，表示真阳性率与假阳性率之比。LR+=se/(1-sp)

• 阴性似然比：negative-likelihood-ratio，LR-，表示假阴性率与真阴性率之比。LR-=(1-se)/sp

26.3 ROC曲线

诊断试验把受试者分成患病和非患病，肯定是有一个标准的，高于这个标准就被判断为患病，低于这个标准就被判断为非患病。

既然有一个标准，那么这个标准就可以有不同的取值，当这个标准变化时，那么被试验判断为患病和非患病的人数自然也就会发生变化。那么灵敏度和特异度这些指标也会发生变化。所以对于不同的诊断取值（被称为截断值），对应着不同的灵敏度和特异度。

我们以灵敏度(或者1-灵敏度)为纵坐标，特异度为横坐标，把不同截断值下的灵敏度和特异度画在一张图上，并把这些点连接成线，就是ROC曲线。ROC曲线下的面积被称为AUC（area under the curve，AUC）。

AUC的取值范围在0到1之间，ROC曲线下的面积越大，也就是AUC越大，说明分类越准确，当AUC值为1时，说明是完美的分类，当AUC为0.5时，说明和乱猜差不多。

下面用一个简单的例子进行说明。

假如，我想根据ca125的值判定一个人到底有没有肿瘤，找了10个肿瘤患者，20个非肿瘤患者，都给他们测一下ca125，这样就得到了30个ca125的值。

set.seed(20220840)
ca125_1 <- c(rnorm(10,80,20),rnorm(20,50,10))

# 30个人的ca125的值如下
ca125_1
##  [1]  51.88470  82.45907 113.66834  63.49476  98.29077  63.27374  74.25079
##  [8]  80.22945  83.01740  99.17105  42.52889  54.56804  48.88383  65.67865
## [15]  44.73153  45.99028  55.82554  42.79242  60.84917  64.80764  51.11468
## [22]  43.40118  47.03850  44.75943  68.34163  60.83829  53.32599  59.92225
## [29]  46.46360  30.02914

假定前10个人是肿瘤，后20个人是非肿瘤。

outcome <- c(rep(c("肿瘤","非肿瘤"),c(10,20)))
outcome <- factor(outcome,levels = c("肿瘤","非肿瘤"))
outcome
##  [1] 肿瘤   肿瘤   肿瘤   肿瘤   肿瘤   肿瘤   肿瘤   肿瘤   肿瘤   肿瘤  
## [11] 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤
## [21] 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤 非肿瘤
## Levels: 肿瘤 非肿瘤

放在一个表格中方便观看：

df <- data.frame(outcome=outcome,
                 ca125=ca125_1
                 )
psych::headTail(df)
##     outcome  ca125
## 1      肿瘤  51.88
## 2      肿瘤  82.46
## 3      肿瘤 113.67
## 4      肿瘤  63.49
## ...    <NA>    ...
## 27   非肿瘤  53.33
## 28   非肿瘤  59.92
## 29   非肿瘤  46.46
## 30   非肿瘤  30.03

现在如果我们设置ca125>60，判断为肿瘤，ca125≤50判断为非肿瘤，就能得到如下的结果：

df1 <- transform(df, pred = ifelse(ca125>60,"猜他是肿瘤","猜他不是肿瘤"))
df1$pred <- factor(df1$pred,levels = c("猜他是肿瘤","猜他不是肿瘤"))
psych::headTail(df1)
##     outcome  ca125         pred
## 1      肿瘤  51.88 猜他不是肿瘤
## 2      肿瘤  82.46   猜他是肿瘤
## 3      肿瘤 113.67   猜他是肿瘤
## 4      肿瘤  63.49   猜他是肿瘤
## ...    <NA>    ...         <NA>
## 27   非肿瘤  53.33 猜他不是肿瘤
## 28   非肿瘤  59.92 猜他不是肿瘤
## 29   非肿瘤  46.46 猜他不是肿瘤
## 30   非肿瘤  30.03 猜他不是肿瘤

对以上结果稍加整理，就能得出一个四格表：

xtabs(~pred+outcome,data = df1)
##               outcome
## pred           肿瘤 非肿瘤
##   猜他是肿瘤      9      5
##   猜他不是肿瘤    1     15

这个表格就是诊断实验的四格表。

通过这个表格，我们就可以计算灵敏度和特异度等指标了:

特异度=15/(15+5)=0.75
灵敏度=9/(1+9)=0.9

这个表格是以（ca125）60为截断值的，如果我们换一个截断值，那么灵敏度和特异度就会发生变化。

下面我们编写一个函数，让它帮我们计算在不同的截断值下，灵敏度和特异度的值。

cal_roc <- function(df, cutoff){
  df <- transform(df, pred = ifelse(ca125>cutoff,"猜他是肿瘤","猜他不是肿瘤"))
  df$pred <- factor(df$pred,levels = c("猜他是肿瘤","猜他不是肿瘤"))
  tb <- table(df$pred,df$outcome)
  sens <- tb[1,1]/colSums(tb)[1]
  spec <- tb[2,2]/colSums(tb)[2]
  list(sens=sens, spec=spec)
}

阈值设置为60，看看是不是和我们上面的结果一样：

cal_roc(df,60)
## $sens
## 肿瘤 
##  0.9 
## 
## $spec
## 非肿瘤 
##   0.75

可以看到是一样的。

下面就是自己选择多个阈值进行计算，先看下ca125的范围，超出这个范围的阈值没有意义。

range(ca125_1)
## [1]  30.02914 113.66834

下面我们确定截断值的范围在30到113之间，每次都加1，然后使用我们的函数计算不同截断值下的灵敏度和特异度：

# 确定取哪些截断值
cutoff <- seq(30,113, 1)

# 计算不同的灵敏度和特异度
rocs <- purrr::map_dfr(cutoff, cal_roc, df=df)
rocs$cutoff <- cutoff
psych::headTail(rocs)
##   sens spec cutoff
## 1    1    0     30
## 2    1 0.05     31
## 3    1 0.05     32
## 4    1 0.05     33
## 5  ...  ...    ...
## 6  0.1    1    110
## 7  0.1    1    111
## 8  0.1    1    112
## 9  0.1    1    113

这样我们就得到了不同截断值下的灵敏度和特异度。

有了这个结果后，我们就可以自己画出ROC曲线了，以1-特异度为横坐标，灵敏度为纵坐标：

library(ggplot2)

ggplot(rocs, aes(1-spec,sens))+
  geom_point(size=2,color="red")+
  geom_path()+
  coord_fixed()+
  theme_bw()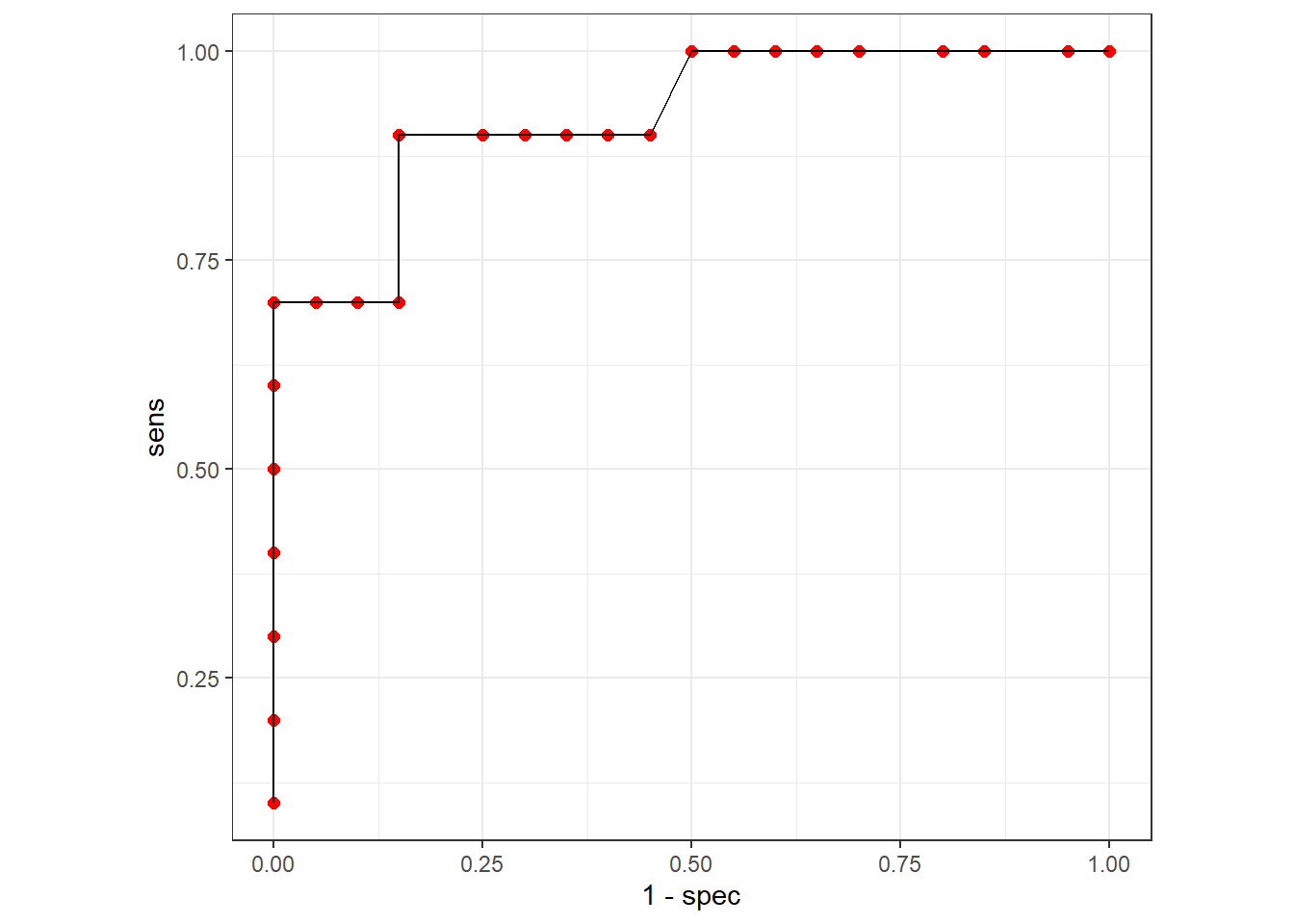

这就是ROC曲线了。

因为不同的截断值对应着不同的灵敏度和特异度，那么肯定就存在一个最佳截断值的问题，一般情况下，使约登指数最大的那个截断值，就是最佳截断值。

• 约登指数=灵敏度+特异度-1

此时的灵敏度+特异度最大，同时也是ROC曲线下的面积（即AUC）最大。

如何寻找这个最佳的截断值呢？当然是挨个试了！但是借助计算机，这个过程一瞬间就完成了。

26.4 用R包绘制ROC

R语言中有非常多的方法可以实现ROC曲线，但是基本上都是至少需要2列数据，一列是真实结果，另一列是预测值（或者叫截断值、阈值、指标等），有了这两列数据，就可以轻松使用各种方法画出ROC曲线并计算AUC。这里给大家介绍这个用的最多的pROC包。

pROC包中提供了一个aSAH数据集，这是一个动脉瘤性蛛网膜下腔出血的数据集，一共113行，7列。其中outcome列是结果变量，1代表Good，2代表Poor：

• gos6：格拉斯哥量表评分
• outcome：结果变量
• gender：性别
• age：年龄
• wfns：世界神经外科医师联合会公认的神经学量表评分
• s100b：生物标志物
• ndka：生物标志物

library(pROC)

str(aSAH)
## 'data.frame':    113 obs. of  7 variables:
##  $ gos6   : Ord.factor w/ 5 levels "1"<"2"<"3"<"4"<..: 5 5 5 5 1 1 4 1 5 4 ...
##  $ outcome: Factor w/ 2 levels "Good","Poor": 1 1 1 1 2 2 1 2 1 1 ...
##  $ gender : Factor w/ 2 levels "Male","Female": 2 2 2 2 2 1 1 1 2 2 ...
##  $ age    : int  42 37 42 27 42 48 57 41 49 75 ...
##  $ wfns   : Ord.factor w/ 5 levels "1"<"2"<"3"<"4"<..: 1 1 1 1 3 2 5 4 1 2 ...
##  $ s100b  : num  0.13 0.14 0.1 0.04 0.13 0.1 0.47 0.16 0.18 0.1 ...
##  $ ndka   : num  3.01 8.54 8.09 10.42 17.4 ...

假如我们想使用s100b这个指标作为我们的截断值，来判断结局到底是good还是poor，根据前面的ROC曲线的定义，我们可以绘制一个ROC曲线，使用R包实现非常简单：

# 计算
res <- roc(aSAH$outcome,aSAH$s100b,auc=T)

# 画图
plot(res,auc.polygon=T,auc.polygon.col="steelblue",
     print.auc=T,
     print.auc.x=0.95,print.auc.y=0.9,print.auc.col="firebrick",
     print.auc.cex=2
     )

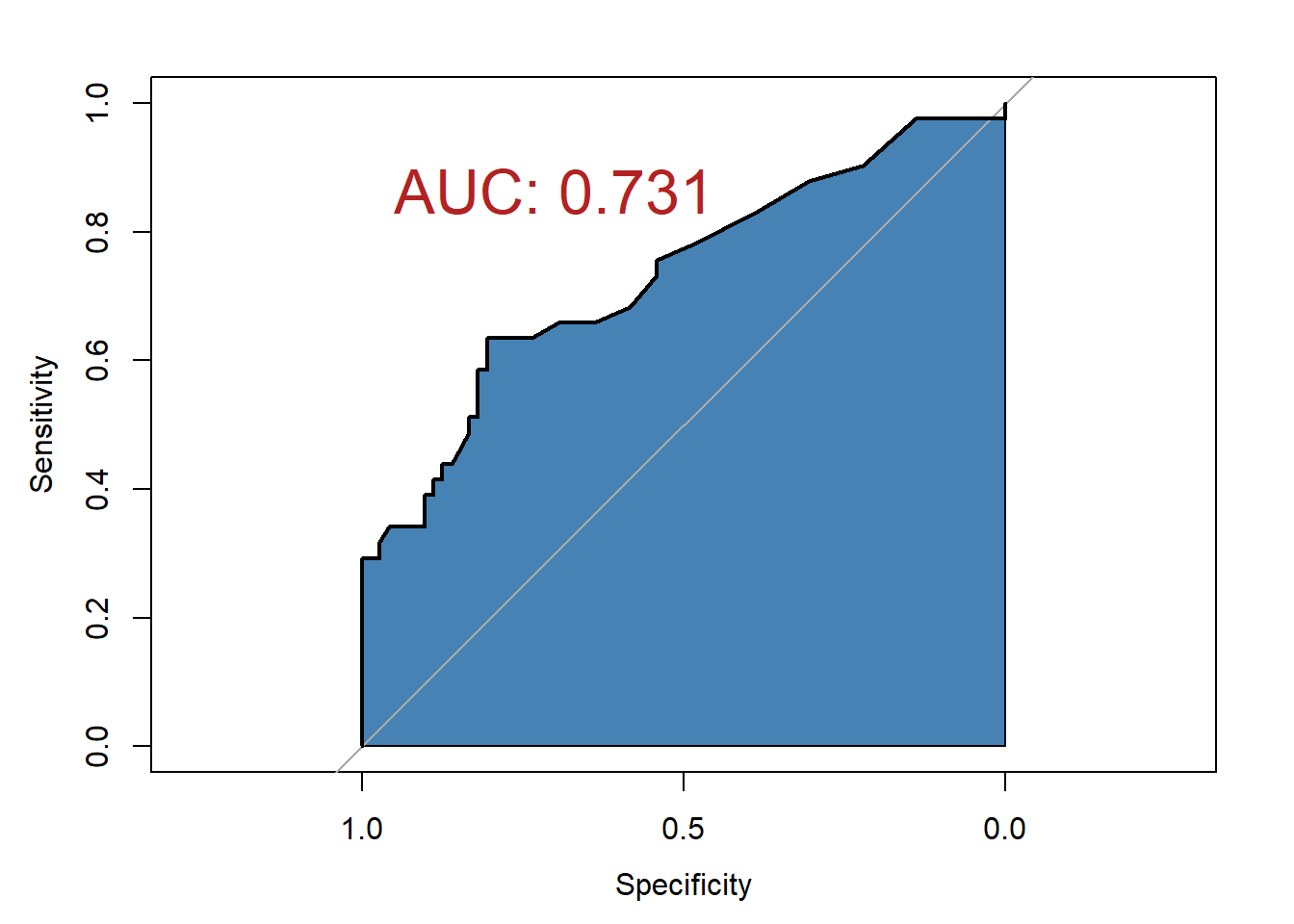
给出的信息非常丰富，不仅画出了图，还给出了ROC曲线下面积（即：AUC）。

# 结果已经存储在res中
res
## 
## Call:
## roc.default(response = aSAH$outcome, predictor = aSAH$s100b,     auc = T)
## 
## Data: aSAH$s100b in 72 controls (aSAH$outcome Good) < 41 cases (aSAH$outcome Poor).
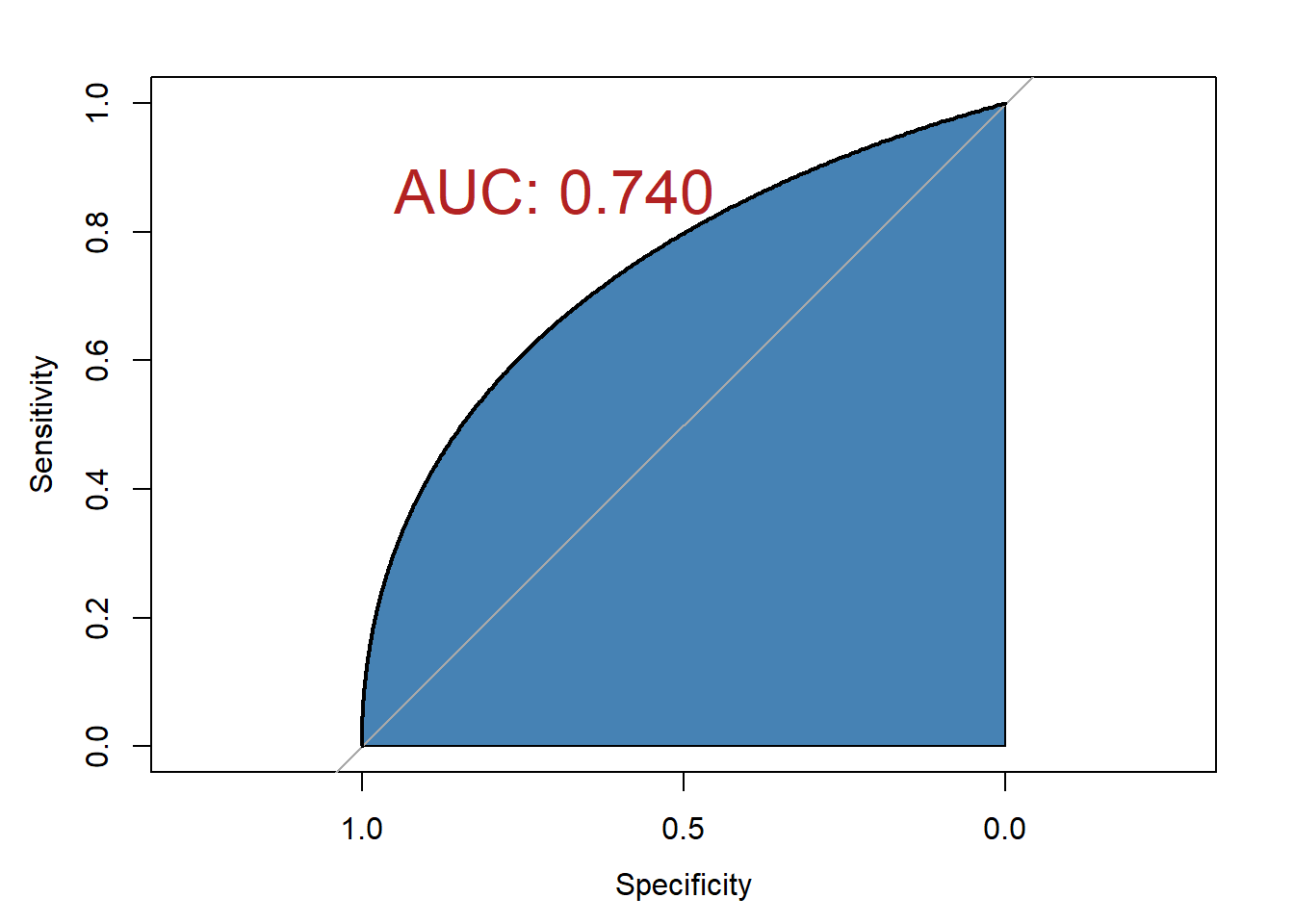
## Area under the curve: 0.7314

课本中还介绍了一种平滑的ROC曲线，在pROC中实现也很简单，添加一个参数即可：

# 计算
res_smooth <- roc(aSAH$outcome,aSAH$s100b,auc=T,smooth=T)

# 画图
plot(res_smooth,auc.polygon=T,auc.polygon.col="steelblue",
     print.auc=T,
     print.auc.x=0.95,print.auc.y=0.9,print.auc.col="firebrick",
     print.auc.cex=2
     )

计算最佳截点也是非常简单的：

plot(res,auc.polygon=T,auc.polygon.col="steelblue",
     legacy.axes = TRUE, # 让x轴从0开始
     print.thres="best") # AUC最大的点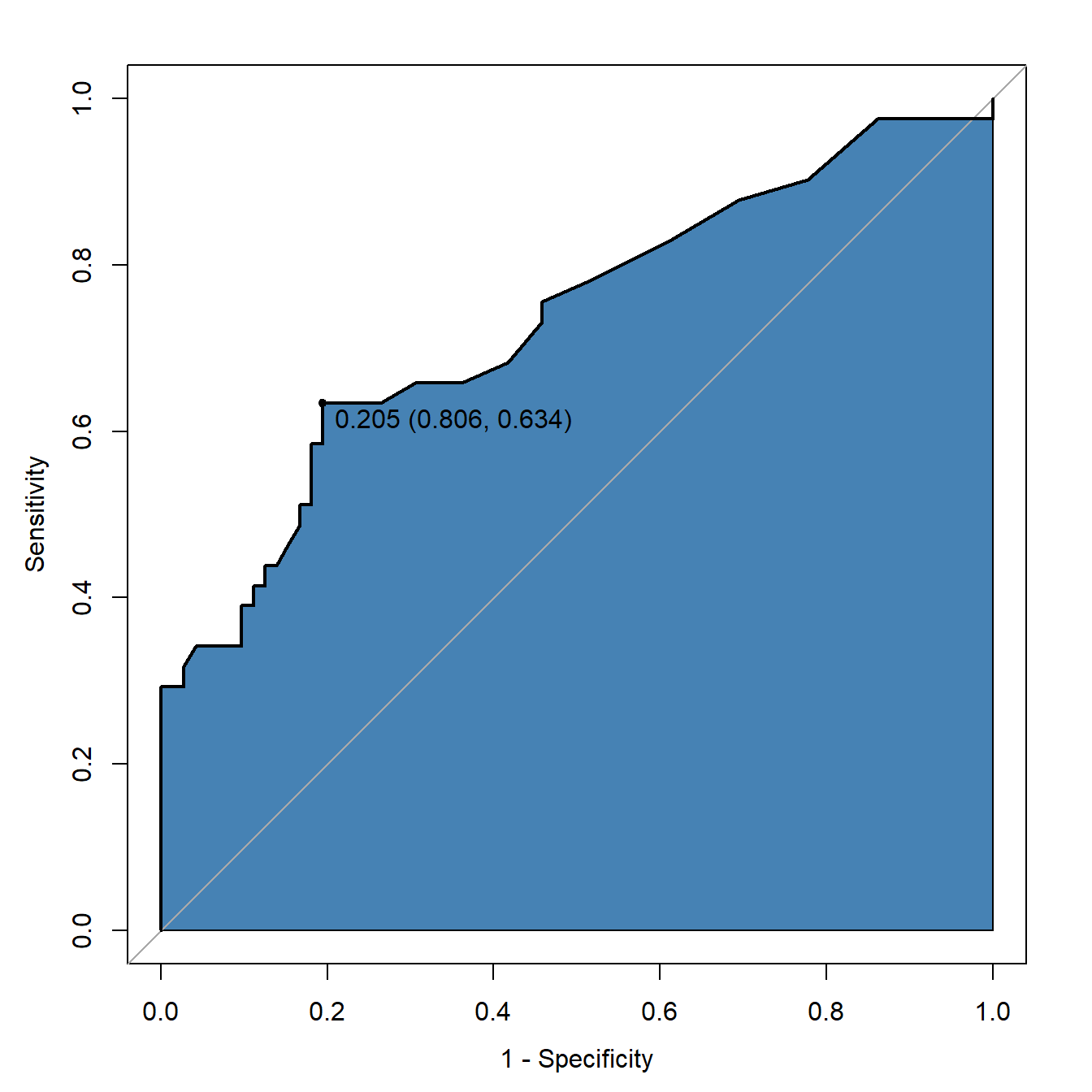

图中的信息显示：最佳截点是0.205，此时的特异度是0.806，灵敏度是0.634，也就是说，当s100b的值是0.205的时候，约登指数最大，同时也是曲线下面积（AUC）最大。

细心的朋友可以可能已经注意到了，上面的ROC曲线的x轴，有的是0-1，有的是1-0，这两种情况都是对的，没必要纠结哈。

26.5 预测模型和ROC

了解了ROC曲线的原理后，使用起来就比较简单了。

以二分类数据为例，如果是在机器学习和临床预测模型中，模型也会对我们的数据作出一个判断，对于每一个样本，模型都会给出两种类型的判断结果，一种是直接给出类别，另一种是给出每种类别的概率，如下所示：

真实类别	预测类别	预测为阳性的概率	预测为阴性的概率
阳性	阳性	0.6	0.4
阳性	阳性	0.7	0.3
阴性	阳性	0.8	0.2
阳性	阴性	0.4	0.6
阴性	阴性	0.2	0.8
阴性	阴性	0.25	0.75
阴性	阴性	0.32	0.68
阳性	阳性	0.7	0.3

这个概率就是我们的截断值，取不同的概率阈值，就会得到不同的分类结果，我们可以规定当概率大于0.5判断为阳性，也可以规定概率大于0.8判断为阳性。所以不同的概率阈值，也对应着不同的灵敏度和特异度，据此就可以绘制出ROC曲线了。

在实际使用时，我们可以借助多种R包帮我们实现”根据不同的阈值计算计算灵敏度/特异度并绘图”的过程，并不需要自己计算，常用的R包有：ROCR、pROC、yardstick等。

除此之外，ROC曲线既然是通过不同的截断值实现的，那么就必然存在最佳截点的问题；对于生存分析来说，也涉及到time-dependent-ROC等问题；为了增加检验可信度，还有bootstrap-ROC等；还有多分类的ROC曲线等，这些问题可参考以下推文：

• 多时间点和多指标的ROC曲线
• 临床预测模型之二分类资料ROC曲线的绘制
• 临床预测模型之生存资料ROC曲线的绘制
• ROC曲线(AUC)的显著性检验
• 生存资料ROC曲线的最佳截点和平滑曲线
• ROC曲线纯手工绘制
• R语言计算AUC(ROC曲线)的注意事项
• ROC阴性结果还是阳性结果
• 多指标联合诊断的ROC曲线
• ROC曲线最佳截点
• bootstrap ROC/AUC
• R语言多分类ROC曲线绘制

公众号后台回复ROC即可获取以上合集链接。