32 竞争风险模型的校准曲线

之前介绍过一次竞争风险模型：Fine-Gray检验、竞争风险模型、列线图绘制,主要是借助cmprsk这个包实现的，并且列线图的绘制也是间接实现的。

今天介绍的QHScrnomo依赖于rms，cmprsk,Hmisc等包，专门用于竞争风险模型的列线图绘制，除此之外还可以建立模型、绘制校准曲线、进行内外部验证等。

32.1 安装

2选1：

devtools::install_github("ClevelandClinicQHS/QHScrnomo")
install.packages("QHScrnomo")

32.2 准备数据

使用casebase中的bmtcrr数据，只使用其中的一部分，并且把字符型变成因子型。

library(QHScrnomo)

data("bmtcrr",package = "casebase")
bmtcrr[,c(1,2,3,6)] <- lapply(bmtcrr[,c(1,2,3,6)],as.factor)
str(bmtcrr)
## 'data.frame':    177 obs. of  7 variables:
##  $ Sex   : Factor w/ 2 levels "F","M": 2 1 2 1 1 2 2 1 2 1 ...
##  $ D     : Factor w/ 2 levels "ALL","AML": 1 2 1 1 1 1 1 1 1 1 ...
##  $ Phase : Factor w/ 4 levels "CR1","CR2","CR3",..: 4 2 3 2 2 4 1 1 1 4 ...
##  $ Age   : int  48 23 7 26 36 17 7 17 26 8 ...
##  $ Status: int  2 1 0 2 2 2 0 2 0 1 ...
##  $ Source: Factor w/ 2 levels "BM+PB","PB": 1 1 1 1 1 1 1 1 1 1 ...
##  $ ftime : num  0.67 9.5 131.77 24.03 1.47 ...

32.3 拟合竞争风险模型

先使用rms拟合cox回归模型，这几个变量只是我为了演示随便挑选的，可能并不是完全适合。

dd <- datadist(bmtcrr)
options(datadist = "dd")

# 对Age这个变量进行样条变换
fit <- cph(Surv(ftime,Status == 1) ~ Sex + rcs(Age,3)+D+Phase, data = bmtcrr,
           x = TRUE, y= TRUE, surv=TRUE, time.inc = 24)

拟合好之后再使用crr.fit变为竞争风险模型，其实是借助了cmprsk::crr：

crr <- crr.fit(fit = fit, cencode = 0, failcode = 1)
class(crr)
## [1] "cmprsk" "crr"
summary(crr)
##              Effects              Response : Surv(ftime, Status == 1) 
## 
##  Factor              Low High Diff. Effect    S.E.    Lower 0.95 Upper 0.95
##  Age                 20  40   20    -0.337350 0.23489 -0.79772    0.12303  
##   Hazard Ratio       20  40   20     0.713660      NA  0.45035    1.13090  
##  Sex - F:M            2   1   NA     0.022279 0.28692 -0.54007    0.58463  
##   Hazard Ratio        2   1   NA     1.022500      NA  0.58271    1.79430  
##  D - ALL:AML          2   1   NA     0.363100 0.29546 -0.21599    0.94219  
##   Hazard Ratio        2   1   NA     1.437800      NA  0.80575    2.56560  
##  Phase - CR1:Relapse  4   1   NA    -1.135800 0.37803 -1.87670   -0.39488  
##   Hazard Ratio        4   1   NA     0.321160      NA  0.15309    0.67376  
##  Phase - CR2:Relapse  4   2   NA    -1.034200 0.35885 -1.73750   -0.33084  
##   Hazard Ratio        4   2   NA     0.355520      NA  0.17596    0.71832  
##  Phase - CR3:Relapse  4   3   NA    -0.914910 0.58559 -2.06260    0.23282  
##   Hazard Ratio        4   3   NA     0.400550      NA  0.12712    1.26220

可以用方差分析看看各个系数的显著性：

anova(crr)
##                 Wald Statistics          Response: Surv(ftime, Status == 1) 
## 
##  Factor     Chi-Square d.f. P     
##  Sex         0.01      1    0.9381
##  Age         2.25      2    0.3238
##   Nonlinear  0.04      1    0.8510
##  D           1.51      1    0.2191
##  Phase      14.70      3    0.0021
##  TOTAL      19.86      7    0.0059

32.4 内部验证

建立好模型之后，可以用tenf.crr对验证集进行交叉验证，查看感兴趣时间点的预测结果(死亡概率)，就相当于内部验证。

# 默认10折交叉验证
set.seed(123)
#可以计算线性预测值，可查看帮助文档
bmtcrr$preds.tenf <- tenf.crr(crr, time = 36, trace = FALSE)
str(bmtcrr$preds.tenf)
##  num [1:177] 0.485 0.171 0.284 0.299 0.206 ...

结果是第36个月的时候，各个病人的死亡风险，而且是考虑到了竞争风险事件的。

32.5 计算C-index

基于上面计算出的概率，计算cindex：

cindex(prob = bmtcrr$preds.tenf,
       fstatus = bmtcrr$Status,
       ftime = bmtcrr$ftime,
       type = "crr",
       failcode = 1, cencode = 0
       )
##            N            n       usable   concordant       cindex 
##  177.0000000  177.0000000 8249.0000000 5092.0000000    0.6172869

cindex=0.617，说明模型一般。

32.6 校准曲线

也是基于上面计算出的cindex。

groupci(x = bmtcrr$preds.tenf,
        ftime = bmtcrr$ftime,
        fstatus = bmtcrr$Status,
        g = 5, # 分成几组
        u = 36, # 时间点
        failcode = 1,
        xlab = "Predicted 3-year mortality",
        ylab = "Actual 3-year mortality"
        )

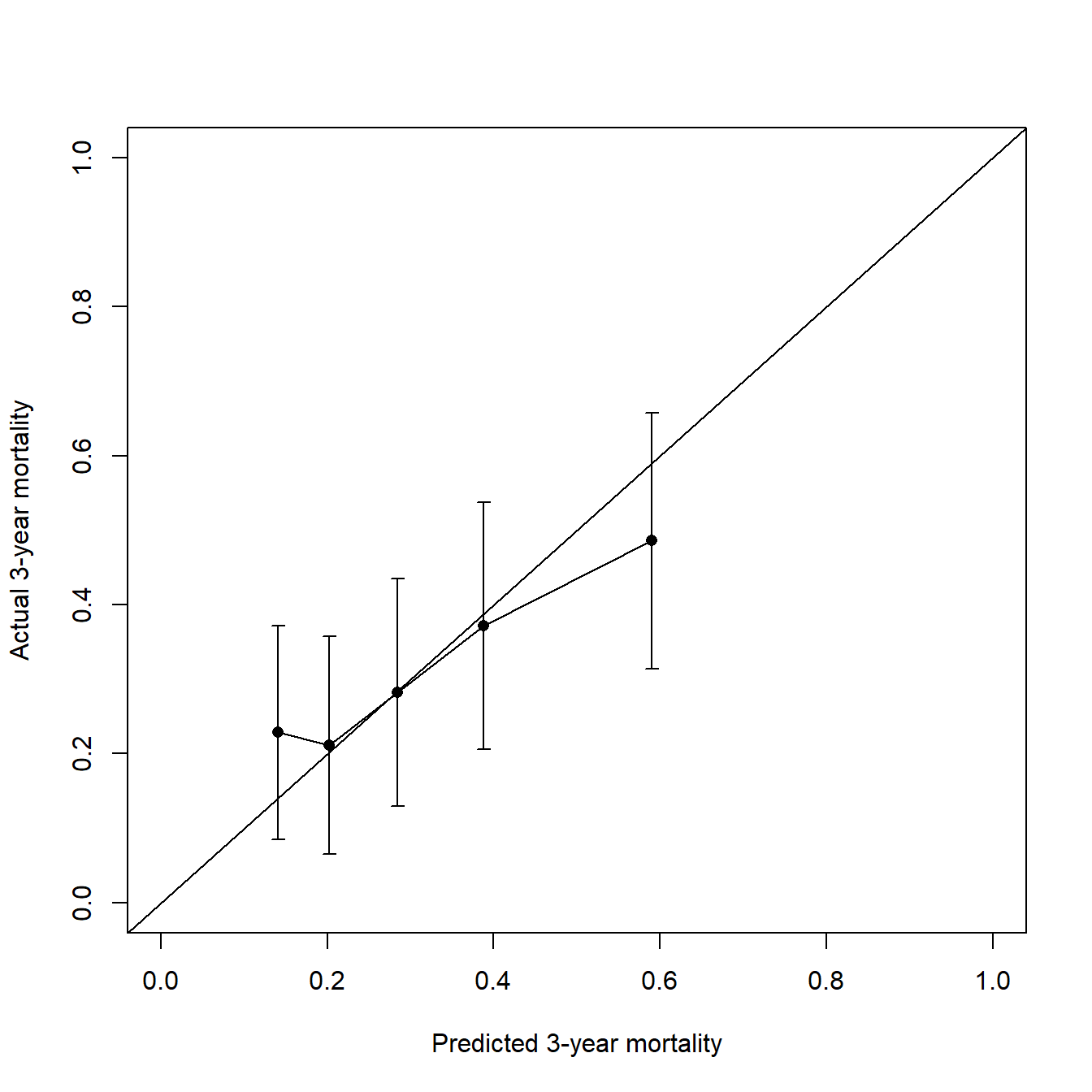
##              x  n events        ci    std.err
## [1,] 0.1408630 36      8 0.2286706 0.07313371
## [2,] 0.2021363 35      7 0.2114286 0.07429595
## [3,] 0.2841367 36     10 0.2822421 0.07775400
## [4,] 0.3876848 35     14 0.3714286 0.08458920
## [5,] 0.5899486 35     17 0.4857143 0.08757744

这个其实就是内部验证的校准曲线了，看起来还不错，因为是在训练集中，训练集的校准曲线其实说明不了任何问题。

如果你觉得不好看可以使用给出的数据自己画，或者直接自己计算也可。可信区间是95%CI，可以通过pred.ci计算的。

32.7 列线图

建立列线图，和rms包的使用一模一样：

nomogram.crr(
  fit = crr,
  failtime = 36,
  lp = T,
  xfrac = 0.65,
  fun.at = seq(0.2, 0.45, 0.05),
  funlabel = "Predicted 3-year risk"
)

32.8 生成模型方程

可以直接给出某个时间点的线性预测值的计算方程：

sas.cmprsk(crr,time = 36)
## Base failure probability by time = 36 is 0.3308 
## - 0.022279144 * (Sex = "M") - 0.012796928 * Age - 
##     6.6881995e-06 * max(Age - 15.6, 0)**3 + 1.140514e-05 * max(Age - 
##     29, 0)**3 - 4.7169407e-06 * max(Age - 48, 0)**3 - 0.36310183 * 
##     (D = "AML") + 0.10164664 * (Phase = "CR2") + 0.22089946 * 
##     (Phase = "CR3") + 1.1358137 * (Phase = "Relapse")

32.9 外部验证（测试集）

直接predict即可：

test_df <- head(bmtcrr,50)#取前50个作为测试集
prob <- predict(crr, time = 36, newdata = test_df)
head(prob)
## [1] 0.4344841 0.2052952 0.3610625 0.2712397 0.2336076 0.6261795

有了概率又可以计算cindex了：

cindex(prob = prob,
       fstatus = test_df$Status,
       ftime = test_df$ftime
       )
##           N           n      usable  concordant      cindex 
##  50.0000000  50.0000000 630.0000000 454.0000000   0.7206349

还可以绘制校准曲线：

groupci(x = prob,
        ftime = test_df$ftime,
        fstatus = test_df$Status,
        u = 36,
        g = 5
        )

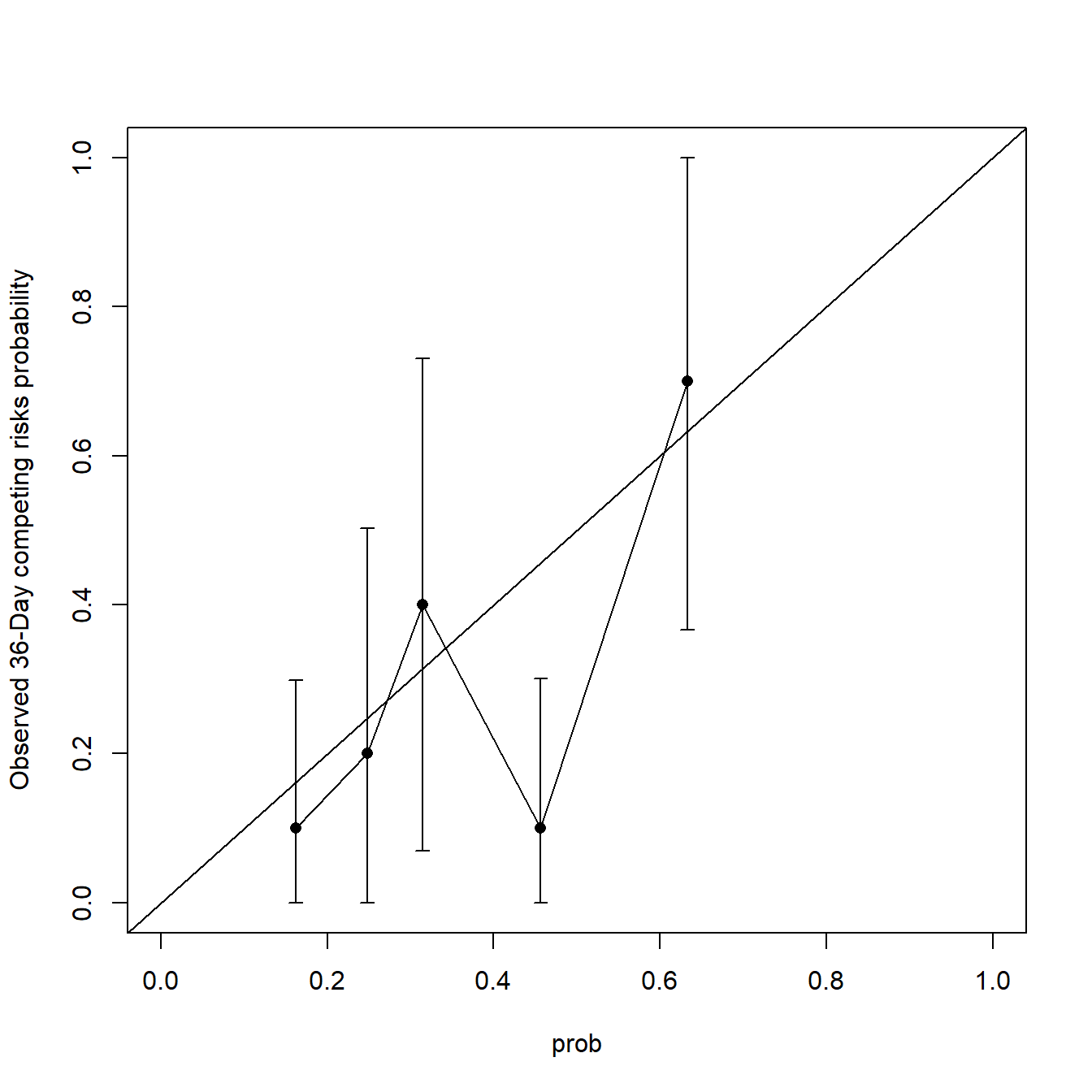
##              x  n events  ci   std.err
## [1,] 0.1619231 10      1 0.1 0.1013889
## [2,] 0.2478567 10      2 0.2 0.1545392
## [3,] 0.3141252 10      4 0.4 0.1683094
## [4,] 0.4561951 10      1 0.1 0.1023904
## [5,] 0.6326698 10      7 0.7 0.1702254

是不是很easy呢。

32.10 参考资料

https://github.com/ClevelandClinicQHS/QHScrnomo
vignette(“QHScrnomo”)