lrm(formula = dead ~ birth + lowph + pltct + bwt + vent + black +
white, data = tmp, x = T, y = T)
Coef S.E. Wald Z Pr(>|Z|)
Intercept 38.3815 11.0303 3.48 0.0005
birth -0.1201 0.0914 -1.31 0.1890
lowph -4.1451 1.1881 -3.49 0.0005
pltct -0.0017 0.0019 -0.91 0.3644
bwt -0.0031 0.0006 -5.14 <0.0001
vent=1 2.7526 0.7436 3.70 0.0002
black 1.1974 0.8448 1.42 0.1564
white 0.8597 0.8655 0.99 0.3206
## 新的
lrm(formula = dead == 1 ~ birth + lowph + pltct + bwt + vent + race, data = tmp)
Coef S.E. Wald Z Pr(>|Z|)
Intercept 39.5788 11.0070 3.60 0.0003
birth -0.1201 0.0914 -1.31 0.1890
lowph -4.1451 1.1881 -3.49 0.0005
pltct -0.0017 0.0019 -0.91 0.3644
bwt -0.0031 0.0006 -5.14 <0.0001
vent=1 2.7526 0.7436 3.70 0.0002
race=other -1.1974 0.8448 -1.42 0.1564
race=white -0.3377 0.2953 -1.14 0.2529 9 列线图的本质
9.1 列线图与模型的关系
前面我们展示了绘制逻辑回归和cox回归列线图的多种方法,不知道大家有没有考虑过,其他模型可以绘制列线图吗?例如lasso回归、随机森林等(不行哈,理论可行,实际不行)。这就涉及到列线图到底是怎么绘制出来的。
对于一个含有多个自变量和1个因变量的逻辑回归来说,回归方程可以写成类似 y=a + b1x1 + b2x2 + b3x3 这种形式,其中b是回归系数。列线图就是把回归方程用图形的方式展现出来,线段的长短(分数)根据回归系数计算。
9.2 列线图分数的计算方法
以下面这个列线图为例:
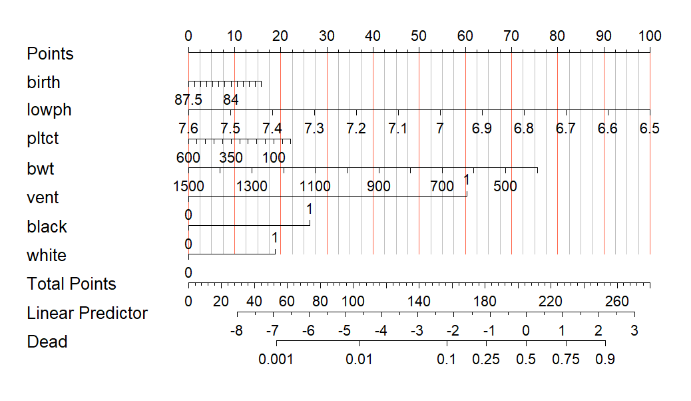
上面这个列线图是一个逻辑回归的,它的逻辑回归的结果是这样的:
在最下面列出了每个自变量的回归系数,我们首先把回归系数绝对值最大的设置为100分,在这个例子中是lowph,它的回归系数绝对值是4.1451,也就是对应的是100分,然后其他自变量都是根据lowph进行转换,即可算出其他自变量对应的得分!
然后根据这个表达式得到的列线图的结果是这样的:
nom1
Points per unit of linear predictor: 21.93145
Linear predictor units per point : 0.04559661
birth Points
81.5 16
82.0 14
82.5 13
83.0 12
83.5 11
84.0 9
84.5 8
85.0 7
85.5 5
86.0 4
86.5 3
87.0 1
87.5 0
lowph Points
6.5 100
6.6 91
6.7 82
6.8 73
6.9 64
7.0 55
7.1 45
7.2 36
7.3 27
7.4 18
7.5 9
7.6 0
pltct Points
0 22
50 20
100 18
150 17
200 15
250 13
300 11
350 9
400 7
450 6
500 4
550 2
600 0
bwt Points
400 76
500 69
600 62
700 55
800 48
900 41
1000 34
1100 27
1200 21
1300 14
1400 7
1500 0
vent Points
0 0
1 60
race Points
black 26
other 0
white 19
Total Points Dead
53 0.001
104 0.010
157 0.100
181 0.250
205 0.500
229 0.750
253 0.900上面的 Linear predictor units per point: 0.04559661 意思是每一个小刻度代表的分数是0.04559661分,这实际上是最大回归系数的1/100(这里应该是4.1451/100=0.041451,实际上会有偏差!)。
9.2.1 分类变量分数的计算
以vent为例,vent=1的时候,它的回归系数是2.7526,那么它对应的分数应该是 2.7526/0.04559661 * 100 ≈ 60,上面得到的结果是60分,一样的!black应该是 1.1974/0.04559661 * 100 ≈ 26,也和我们算的差不多!
这就是分类变量分数的计算。
9.2.2 连续性变量分数的计算
连续性自变量需要考虑取值范围,它的解释应该是每增加一个单位,因变量变化多少,对于pltct来说,系数是-0.0017,就是每增加1各单位,因变量减少0.0017。
pltct是600,对应的分数是0分,那么如果是100,对应的分数就是 (600-100)* (0.0017/0.04559661) ≈ 18。
这就是连续性变量分数的计算。
了解了列线图的分数计算方法,即使没有R语言,你也可以通过手动计算算出来,这样你可以自己画图!(理论上可行,但实际上很难,至少我还没见到过…)